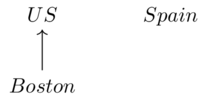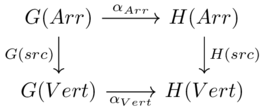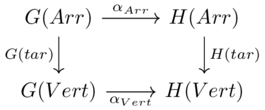Seven Sketches in Compositionality(416)
By David Spivak and Brendan Fong [1].
Chapter 1: Generative Effects(86)
More than the sum of their parts(6)
A first look at generative effects(3)
Central theme of category theory: study of structures and structure-preserving maps.
Asking which aspects of structure one wants to preserve becomes the question "what category are you working in?".
Example: there are many functions \(\mathbb{R} \xrightarrow{f} \mathbb{R}\), which we can think of observations (rather than view \(x\) directly we only view \(f(x)\)). Only some preserve the order of numbers, only some preserve distances between numbers.
The less structure that is preserved by our observation of a system, the more ’surprises’ when we observe its operations - call these generative effects.
Consider a world of systems which are points which may or may not be connected. There are 5 partitionings or systems of three points.
Suppose Alice makes observations on systems with a function \(\phi\) which returns whether or not points are connected. Alice also has an operation on two systems called join which puts two points in the same partition if they are connected in either of the original systems.
Alice’s operation is not preserved by the join operation.
Application: Alice is trying to address a possible contagion and needs to know whether or not it is safe to have each region extract their data and then aggregate vs aggregating data and then extracting from it.
Exercise 1-1(2)
Give an example and non-example for
an order-preserving function
a metric-preserving function
an addition-preserving function
Solution(1)
Order-preserving \(x+1\), non-order-preserving \(-x\)
Metric preserving \(x+1\), non-metric-preserving \(2x\)
Addition-preserving \(2x\), non-addition-preserving \(x^2\)
Linked by
Ordering systems(3)
The operation of joining systems earlier can be derived from a more basic structure: order.
Let \(A \leq B\) be defined as a relationship that holds when \(\forall x,y:\ (x,y) \in A \implies (x,y) \in B\)
The joined system \(A \lor B\) is the smallest system that is bigger than both \(A\) and \(B\).
The possibility of a generative effect is captured in the inequality \(\phi(A) \lor \phi(B) \leq \phi(A \lor B)\), where \(\phi\) was defined earlier.
There was a generative effect because there exist systems violate this (both are individually false for \(\phi\) but not when put together).
\(\phi\) preserves order but not join
Exercise 1-7(2)
Using the order \(false \leq true\) for \(\mathbb{B}\), what is:
\(true \lor false\)
\(false \lor true\)
\(true \lor true\)
\(false \lor false\)
Solution(1)
This is same as logical or: \(true,\ true,\ true,\ false\)
What is order(11)
Review of sets, relations functions(1)
Basic review of set, subset, partition, equivalence relation.
A partition of a set is a surjective map to the parts.
Any \(a \in A\) can be thought of as a function \(\{1\} \xrightarrow{a} A\)
Exercise 1-16(2)
Suppose \(A\) is a partitioned set and \(P,Q\) are two partitions such that for each \(p \in P\) there exists a \(q \in Q\) with \(A_p=A_q\)
Show that for each \(p \in P\) there is at most one \(q \in Q\) such that \(A_p = A_q\)
Show that for each \(q \in Q\) there is a \(p \in P\) such that \(A_p = A_q\)
Solution(1)
Suppose \(q' \ne q\). If they are both equal to \(A_p\) then they are equal to each other, but a partition rule is that \(q' \ne q\) must have an empty intersection (and \(A_p\) cannot be empty by the other rule).
By part 1, the mapping between part labels is a bijection, so there is an inverse map as well.
Exercise 1-20(2)
Finish proof Proposition 1.19. Suppose that \(\sim\) is an equivalence relation on a set A, and let P be the set of \(\sim\)-closed and \(\sim\)-connected subsets.
Show that each part \(A_p\) is nonempty
Show that \(p \ne q \implies A_p \cap A_q = \varnothing\)
Show that \(A = \bigcup_{p \in P} A_p\)
Proof(1)
Part of the definition of \(\sim\)-connected is being nonempty
Suppose \(a \in A\) is in the intersection. Then \(a \sim p\) and \(a \sim q\) for some elements \(p \not\sim q\) arbitrarily selected from \(A_p, A_q\). But this is impossible because \(\sim\) is transitive, so this must be impossible.
Every \(a \in A\) is part of some equivalence class which is a \(\sim\)-closed and \(\sim\)-connected set, so \(A \subseteq \bigcup_{p \in P} A_p\)
The equivalence class is \(\sim\)-closed because two elements being \(\sim\)-related implies they are in the same equivalence class.
The equivalence class is \(\sim\)-connected because equivalence classes are nonempty and the equivalence relation is transitive.
The constituents of \(A_p\) were defined to be subsets of \(A\), so unioning these will also be a subset of \(A\), i.e. \(\bigcup_{p \in P} A_p \subseteq A\).
Therefore \(A = \bigcup_{p \in P} A_p\).
Function(1)
A function from \(S\) to \(T\)
A relation \(F \subseteq S \times T\) such that \(\forall s \in S:\ \exists! t \in T:\ (s,t) \in F\)
The preimage of an element \(t \in T\) is \(\{s \in S\ |\ F(s)=t\}\)
\(\hookrightarrow\) Injectivity: \(s\ne s' \implies F(s)\ne F(s')\)
\(\twoheadrightarrow\) Surjectivity: \(\forall t \in T:\ \exists s \in S:\ (s,t) \in F\)
\(\xrightarrow \cong\) Bijectivity: both injectivity and surjectivity.
Linked by
Partition(1)
A partition of set \(A\)
A set \(P\) (‘part labels’) and, for each \(p \in P\), a nonempty subset (‘pth part’) \(A_p \subseteq A\) such that:
\(A = \bigcup_{p \in P}A_p\)
\(p \ne q \implies A_p \cap A_q = \varnothing\)
Two partitions are considered the same if the partitioned groups are the same, the labels don’t matter.
Linked by
Partitions are equivalences(2)
There is a bijection between ways to partition a set \(A\) and the equivalence relations on \(A\)
Proof(1)
Every partition gives rise to a distinct equivalence relation
Define \(a \sim b\) to mean \(a,b\) are in the same part. This is a reflective, symmetric, and transitive relation given the definition of a partition.
Every equivalence relation gives rise to a distinct partition.
Define a subset \(X \subseteq A\) as \(\sim\)-closed if, for every \(x \in X\) and \(x' \sim x\), we have \(x' \in X\).
Define a subset \(X \subseteq A\) as \(\sim\)-connected if it is nonempty and \(\forall x,y \in X:\ x \sim y\)
The parts corresponding to \(\sim\) are precisely the \(\sim\)-closed and \(\sim\)-connected subsets.
Linked by
Quotient(1)
A quotient of a set under an equivalence relation.
This is equivalent to the parts of the partition associated with the equivalence relation.
Linked by
Relation(1)
A relation between sets \(X\) and \(Y\)
A subset \(R \subseteq X \times Y\).
A binary relation on \(X\) is a subset of \(X \times X\)
Linked by
Preorders(10)
Preorders are just equivalence relations without the symmetric condition.
Every set can be considered as a discrete preorder with the binary relation of equality. Also the trivial opposite (codiscrete preorder) where all pairs are in the relation.
Every graph yields a preorder on the vertices where \(v \leq w\) iff there is a path from \(v\) to \(w\).
Reflexive because of length-0 paths, transitive because of path concatenation.
Product of two preorders can be considered as a preorder by only comparing things when both preorders independently agree on the pairs.
Preorder(1)
A preorder / partial order / total order relation on a set \(X\)
Preorder: a binary relation on \(X\) that is reflexive and transitive.
A partial order (poset) has the additional constraint that \(x \leq y \land y \leq x \implies x=y\)
We can always get a partial order from a preorder by quotienting, so it’s not that special.
A total order has all elements comparable.
Linked by
- Exercise 1-55: referenced
- Opposite preorder: referenced
- Skeletality: referenced
- Upper set: referenced
- Monotone maps: referenced
- Monotone maps: referenced
- Monotone map: referenced
- Exercise 1-66: referenced
- Identities are monotone: referenced
- Exercise 1-85: referenced
- Meets of subsets: referenced
- Galois connection: referenced
- Adjoint functor theorem for preorders: referenced
- Bool-category: referenced
- Preorders are Bool-categories: referenced
- Proof: referenced
- Proof: referenced
- Exercise 2-67: referenced
- Exercise 2-67: referenced
- Solution: referenced
- Galois connections are adjoint: referenced
- Adjoint examples: referenced
- Exercise 3-81: referenced
- Solution: referenced
- Exercise 3-88: referenced
- Exercise 3-90: referenced
- Can we build it: referenced
- Can we build it: referenced
- Can we build it: referenced
- Feasibility relationships as Bool-profunctors: referenced
- Feasilibiliy relation: referenced
- Feasilibiliy relation: referenced
- Monoidal categories: referenced
Exercise 1-53(2)
For any set \(S\) there is a coarsest partition having just one part.
What surjective function does this correspond to?
(Likewise for the finest partition?)
Solution(1)
The trivial map to \(\{1\}\) and the identity, respectively.
Exercise 1-55(2)
Prove that the upper sets on a discrete preorder for some set \(X\) is simply the power set \(P(X)\)
Solution(1)
The upper set criterion is satisfied by any subset, thus all possible subsets are upper sets.
The binary relation is equality, thus the upper subset criterion becomes \(p \in U \land p = q \implies q \in U\) or alternatively \(p \in U \implies p \in U\) which is always satisfied.
Graph(1)
A graph (of vertices, arrows)
A tuple \(G=(V, A, s, t)\)
Set of vertices and arrows, with two functions \(A\rightarrow V\) which say where the source and target of each arrow goes to.
A path in \(G\) is any sequence of arrows such that the target of one arrow is the source of the next (including length 0 and 1 sequences).
Linked by
Opposite preorder(1)
An opposite preorder
Given a preorder \((P, \leq)\), we define \(p \leq^{op} q \iff q \leq p\)
Linked by
Skeletality(1)
Categorical skeletality generally means \(x \cong y \implies x = y\)
E.g. a skeletal preorder is a poset.
Linked by
Upper set(1)
An upper set in \(P\) for some preorder \((P, \leq)\)
A subset \(U\) of \(P\) satisfying the condition \(p \in U \land p \leq q \implies q \in U\)
Anything you add to the upper set means you have to add everything greater than it.
Example: the possible upper sets of \(Bool\) are \(\{\varnothing, \{true\}, \{true, false\}\}\)
Linked by
Monotone maps(15)
Category theory emphasizes that preorders themselves (each a minature world, composed of many relationships) can be related to one another.
Monotone maps are important because they are the right notion of structure-preserving map for preorders.
The map (‘cardinality’) sending a power-set (with inclusion ordering) to the natural numbers with standard ordering is a monotone map.
Given a preorder, the inclusion map of the upper sets of \(P\) (ordered by inclusion) to the power set of \(P\) (ordered by inclusion) is a monotone map.
Monotone map(1)
A monotone map between preorders \((A, \leq_A), (B, \leq_B)\)
A function \(A \xrightarrow{f} B\) such that \(\forall x,y \in A: x \leq_A y \implies f(x) \leq_B f(y)\)
Linked by
- Monotone maps: referenced
- Monotone maps: referenced
- Monotone maps: referenced
- Preorder isomorphism: referenced
- Preorder isomorphism: referenced
- Pullback along monotone: referenced
- Exercise 1-66: referenced
- Exercise 1-67: referenced
- Solution: referenced
- Identities are monotone: referenced
- Proof: referenced
- Monotones to bool: referenced
- Proof: referenced
- Back to observations and generative effects: referenced
- Monotone maps that preserve meets: referenced
- Generative effect: referenced
- Exercise 1-94: referenced
- Galois connection: referenced
- Total order galois connections: referenced
- Total order galois connections: referenced
- Basic theory of Galois connections: referenced
- Basic theory of Galois connections: referenced
- Galois connection alternate form: referenced
- Adjoints preserving meets and joins: referenced
- Proof: referenced
- Adjoint functor theorem for preorders: referenced
- Adjoint functor theorem for preorders: referenced
- Proof: referenced
- Adjoints in Set: referenced
- Closure operator: referenced
- Eval as closure: referenced
- Adjunctions from closures: referenced
- Exercise 1-119: referenced
- Solution: referenced
- Monoidal monotone: referenced
- Exercise 2-44: referenced
- Proof: referenced
- Proof: referenced
- Bool-functors: referenced
- SMP currying: referenced
- Exercise 2-82: referenced
- Exercise 2-82: referenced
- Exercise 2-82: referenced
- Solution: referenced
- Solution: referenced
- Proof: referenced
- Functor between preorders: referenced
- Functor between preorders: referenced
- Natural transformations between sequences: referenced
- Natural isomorphism of Bool-categories and preorders: referenced
- Feasibility relationships as Bool-profunctors: referenced
- Feasibility relationships as Bool-profunctors: referenced
- Feasilibiliy relation: referenced
- Solution: referenced
- Companion and conjoint of addition: referenced
Dagger preorder(1)
A dagger preorder
\(q \leq p \iff p \leq q\) - this is tantamount to an equivalence relation.
Linked by
Preorder isomorphism(1)
A preorder isomorphism
A monotone map for which there exists an inverse monotone map (\(f;g=id\) and \(g;f = id\))
If this exists, we say the preorders involved are isomorphic.
Linked by
Pullback along monotone(1)
A pullback along a monotone map \(P \xrightarrow{f} Q\)
We take the preimage of \(f\), but not for a single element of \(Q\) but rather an upper set of \(Q\).
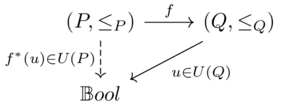
Noting that upper sets are monotone maps to Bool, it follows that the result of a pullback is an upper set in \(P\) follows from the fact that composition preserves monotonicity.
Therefore the type of the pullback is \(U(Q) \xrightarrow{f^*} U(P)\)
Linked by
Exercise 1-66(2)
Let \((P, \leq)\) be a preorder and recall the opposite preorder.
Show that the set \(\uparrow(p) := \{p' \in P\ |\ p \leq p'\}\) is an upper set for any \[p \in P\]
Show that this construction defines a monotone map \((P, \leq^{op}) \xrightarrow{\uparrow} U(P)\)
Show that \(p \leq p' \iff \uparrow(p') \subseteq \uparrow(p)\)
Draw a picture of the map \(\uparrow\) in the case where \(P\) is the preorder \((b\geq a \leq c)\).
Solution(1)
This is the Yoneda lemma for preorders (up to equivalence, to know an element is the same as knowing its upper set).
This is basically the definition an upper set starting at some element.
Interpreting the meaning of the preorder in the domain and codomain of \(\uparrow\), this boils down to showing \(p \leq p'\) implies \(\uparrow(p') \subseteq \uparrow(p)\) - This is shown by noting that \(p' \in \uparrow(p)\) and anything ‘above’ \(p'\) (i.e. \(\uparrow(p')\)) will therefore be in \(\uparrow(p)\).
Forward direction has been shown above - The other direction is shown just by noting that \(p\prime\) must be an element of \(\uparrow(p\prime)\) and by the subset relation also in \(\uparrow(p')\), therefore \(p \leq p'\).

Exercise 1-67(2)
Show that when \(P\) is a discrete preorder, then every function \(P \rightarrow Q\) is a monotone map, regardless of the order \(\leq_Q\).
Solution(1)
The only time the monotonicity criterion is deployed is when two elements of \(P\) are related, and for a discrete category this means we only have to check whether \(f(a) \leq_Q f(a)\), which is true because preorders are reflexive.
Exercise 1-73(2)
Recall skeletal preorders and dagger preorders.
Show that a skeletal dagger preorder is just a discrete preorder (and hence can be identified with a set)
Solution(1)
Because preorders are reflexive, we just have to show \(a \ne b \implies a \not\leq b\), or its contrapositive: \(a \leq b \implies a = b\).
\(a \leq b \overset{dagger}{\implies} b \leq a \overset{skeletal}{\implies} a = b\)
Identities are monotone(2)
For any preorder, the identity function is a monotone map.
The composition of two monotone maps (\(P \xrightarrow{f} Q \xrightarrow{g} R\)) is also monotone.
Proof(1)
Monotonicity translates to \(a \leq b \implies a \leq b\) and is trivially true.
Need to show: \(a \leq_P b \implies g(f(a)) \leq_R g(f(b))\)
The monotonicity of \(f\) gives us \(f(a) \leq_Q f(b)\) and the monotonicity of \(g\) gives us the result we need.
Monotones to bool(2)
Let \(P\) be a preorder. Monotone maps \(P \rightarrow \mathbb{B}\) are in one-to-one correspondance with upper sets of \(P\).
Proof(1)
Let \(P \xrightarrow{f} \mathbb{B}\) be a monotone map. The subset \(f^{-1}(true)\) is an upper set.
Suppose \(p \in f^{-1}(true)\) and \(p \leq q\).
Then \(true = f(p) \leq f(q)\) because \(f\) is monotonic.
But there is nothing strictly greater than \(true\) in \(\mathbb{B}\), so \(f(q) = true\) and therefore \(q \in f^{-1}(true)\) too.
Suppose \(U \in U(P)\), and define \(P\xrightarrow{f_U}\mathbb{B}\) such that \(f_U=true \iff p \in U\)
Given there are only two values in \(B\) and an arbitrary \(p\leq q\), the only way for this to not be monotone is for \(f_U(p) \land \neg f_U(q)\) but this defies the definition of an upper set.
The two constructions are mutually inverse.
Linked by
Meets and joins(14)
Definition and basic examples(9)
There could be multiple meets/joins, but the definition forces them to be isomorphic.
An arbitrary preorder need not have a meet nor join.
E.g a two element discrete preorder has no overall meet/join, because the meet must be less/greater than or equal to both elements in the set.
Exercise 1-85(2)
Let \(p \in P\) be an element in a preorder. Consider \(A = \{p\}\)
Show that \(\wedge A \cong p\)
Show that if \(P\) is a partial order, then \(\wedge A = p\)
Are the analogous facts true when \(\wedge\) is replaced by \(\vee\)?
Solution(1)
The first condition of the meet gives us that \(\wedge A \leq p\).
The second condition is that \(\forall q \in P: q \leq p \implies q \leq \wedge A\).
Substituting \(p\) in for \(q\), the antecedent holds such that we get \(p \leq \wedge A\).
Therefore \(p \cong \wedge A\)
The difference between a partial order and a preorder is that congruent elements are equal, so we directly get that \(p = \wedge A\)
Yes, the argument is perfectly symmetric.
Meet and join(1)
For a preorder \((P, \leq)\), the meet and join of \(A \subseteq P\).
The meet \(\wedge A\) is an element such that
\(\forall a \in A: \wedge A \leq a\)
\(\forall q \in P: (\forall a \in A: q \leq a) \implies q \leq \wedge A\)
Think of as a GREATEST LOWER BOUND
The join \(\vee A\) is an element such that
\(\forall a \in A: a \leq \vee A\)
\(\forall q \in P: (\forall a \in A: a \leq q) \implies \vee A \leq q\)
Think of as a LEAST UPPER BOUND
Linked by
- Solution: referenced
- Meets and joins of bool: referenced
- Meets and joins of bool: referenced
- Meets and joins of powerset: referenced
- Meets and joins of powerset: referenced
- Meets and joins of total order: referenced
- Meets and joins of total order: referenced
- Meets of subsets: referenced
- Back to observations and generative effects: referenced
- Back to observations and generative effects: referenced
- Solution: referenced
- Solution: referenced
- Proof: referenced
- Basic theory of Galois connections: referenced
- Adjoints preserving meets and joins: referenced
- Adjoints preserving meets and joins: referenced
- Adjoints preserving meets and joins: referenced
- Adjoints preserving meets and joins: referenced
- Adjoints preserving meets and joins: referenced
- Proof: referenced
- Adjoint functor theorem for preorders: referenced
- Adjoint functor theorem for preorders: referenced
- Adjoint functor theorem for preorders: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Quantales: referenced
- Quantale: referenced
- Quantale: referenced
- Cost quantale: referenced
- Cost quantale: referenced
- Cost quantale: referenced
- All joins implies all meets: referenced
- All joins implies all meets: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Quantale is SMP with all joins: referenced
- Quantale is SMP with all joins: referenced
- Proof: referenced
- Exercise 2-92: referenced
- Solution: referenced
- Solution: referenced
- Exercise 3-88: referenced
Meets and joins of bool(1)
Meets and joins of total order(1)
In a total order, the meet of a set is its infimum, while the join is the supremum.
Note that \(\mathbb{B}\) is a total order, to generalize Example 1.88.
Meets of subsets(2)
Suppose \((P,\leq)\) is a preorder and \(A \subseteq B \subseteq P\) are subsets that have meets. Then \(\bigwedge B \leq \bigwedge A\)
Solution(1)
Let \(m = \bigwedge A\) and \(n = \bigwedge B\).
For any \(a \in A\) we also have \(a \in B\), so \(n \leq A\) because \(n\) is a lower bound for \(B\).
Thus \(n\) is also a lower bound for \(A\) and hence \(n \leq m\) because \(m\) is \(A\)’s greatest lower bound.
Linked by
Back to observations and generative effects(5)
We are comparing the observation of a combined system or the combination of observations.
The other direction, restricting an observation of a system to a subsystem, does not have problems for monotone maps (which preserve meets, not joins).
Monotone maps that preserve meets(1)
A monotone map \(P \xrightarrow{f} Q\) that preserves meets
\(f(a \land_P b) \cong f(a) \land_Q f(b)\)
Likewise, to preserve joins is for \(f(a \lor_P b) \cong f(a) \lor_Q f(b)\)
Generative effect(1)
A monotone map \(P \xrightarrow{f} Q\) has a generative effect
\(\exists a,b \in P: f(a) \lor f(b) \not\cong f(a \lor v)\)
Linked by
Exercise 1-94(2)
Prove that for any monotone map \(P \xrightarrow{f} Q\):
if there exist \(a \lor b \in P\) and \(f(a) \lor f(b) \in Q\):
\(f(a) \lor_Q f(b) \leq f(a \lor_P b)\)
Solution(1)
Let’s abbreviate \(f(a\ \lor_P\ b)\) as \(JF\) (join-first) and \(f(b)\ \lor_Q\ f(a)\) as \(JL\) (join-last)
This exercise is to show that \(JL \leq JF\)
The property of joins gives us, in \(P\), that \(a\ \leq\ (a \lor b)\) and \(b\ \leq\ (a \lor b)\)
Monotonicity then gives us, in \(Q\), that \(f(a) \leq JF\) and \(f(b) \leq JF\)
We also know from the property of joins, in \(Q\), that \(f(a) \leq JL\) and \(f(b) \leq JL\)
The only way that \(JF\) could be strictly smaller than \(JL\), given that both are \(\geq f(a)\) and \(\geq f(b)\) is for \(f(a) \leq JF < JL\) and \(f(b) \leq JF < JL\)
But, \(JL \in Q\) is the smallest thing (or equal to it) that is greater than \(f(a)\) and \(f(b)\), so this situation is not possible.
Galois connections(30)
Definition and examples(5)
Exercise 1-101(2)
Does \(\mathbb{R}\xrightarrow{\lceil x/3 \rceil}\mathbb{Z}\) have a left adjoint \(\mathbb{Z} \xrightarrow{L} \mathbb{R}\)? If not, why? If so, does its left adjoint have a left adjoint?
Solution(1)
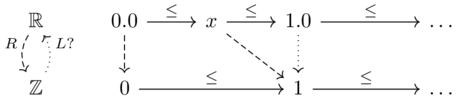
Assume we have an arbitrary left adjoint, \(L\).
For \(x\) as it approaches \(0.0 \in \mathbb{R}\) from the right, we have \(R(x) \leq 1\), therefore \(L(1) \leq x\) because \(L\) is left adjoint.
Therefore \(L(1)\leq 0.0\), yet this implies \(R(0.0) \leq 1\).
This contradicts \(R(0.0)=0\), therefore no left adjoint exists.
Floor and ceil(1)
Consider the map \(\mathbb{Z} \xrightarrow{3z} \mathbb{R}\) which sends an integer to \(3z\) in the reals.
To find a left adjoint for this map, we write \(\lceil r \rceil\) for the smallest natural above \(r \in \mathbb{R}\) and \(\lfloor r \rfloor\) for the largest integer below \(r \in \mathbb{R}\)
The left adjoint is \(\lceil r/3 \rceil\)
Check: \(\lceil x/3 \rceil \leq y\) \(\iff x \leq 3y\)
Galois connection(1)
A Galois connection between preorders \(P\) and \(Q\), and the left and right adjoints of a Galois connection
A pair of monotone maps \(P \xrightarrow{f} Q\) and \(Q \xrightarrow{g} P\) such that:
\(f(p) \leq q \iff p \leq g(q)\)
\(f\) is left adjoint and \(g\) is right adjoint of the Galois connection.
Linked by
- Exercise 1-101: referenced
- Floor and ceil: referenced
- Total order galois connections: referenced
- Total order galois connections: referenced
- Back to partitions: referenced
- Back to partitions: referenced
- Basic theory of Galois connections: referenced
- Galois connection alternate form: referenced
- Galois connection alternate form: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Adjoint functor theorem for preorders: referenced
- Adjoint functor theorem for preorders: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Adjoints in Set: referenced
- Adjoints in Set: referenced
- Exercise 1-110: referenced
- Exercise 1-110: referenced
- Solution: referenced
- Closure operators: referenced
- Adjunctions from closures: referenced
- Adjunctions from closures: referenced
- Exercise 1-119: referenced
- Solution: referenced
- Preorder of relations: referenced
- Preorder of relations: referenced
- Preorder of relations: referenced
- Exercise 1-125: referenced
- Proof: referenced
- Proof: referenced
- Solution: referenced
- Proof: referenced
- Galois connections are adjoint: referenced
Total order galois connections(1)
Consider the total orders \(P = Q = \underline{3}\) with the following monotone maps:
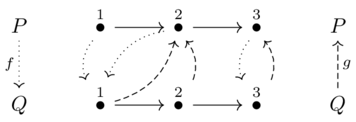
These do form a Galois connection
These maps do not form a Galois connection:
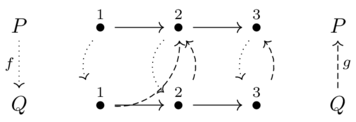
These do not because of \(p=2, q = 1\)
\(f(p)=2 \not \leq q=1\) which is not the same as \(p = 1 \leq g(q)=2\)
In some sense that can be formalized, for total orders the notion of Galois connection corresponds to the maps not ‘crossing over’.
Back to partitions(3)
Given any function \(S \xrightarrow{g} T\), we can induce a Galois connection \(Prt(S) \leftrightarrows Prt(T)\) between the sets of partitions of the domain and codomain.
Determine the left adjoint \(Prt(S) \xrightarrow{g_!} Prt(T)\)
Starting with a given partition in \(S\), obtain a partition in \(T\) by saying two elements, \(t_1,t_2\) are in the same partition if \(\exists s_1 \sim s_2: g(s_1)=t_1 \land g(s_2)=t_2\)
This is not necessarily a transitive relation, so take the transitive closure.
Determine the right adjoint \(Prt(T) \xrightarrow{g^*} Prt(S)\)
Given a partition of \(T\), we say two elements in \(S\) are connected iff \(g(s_1) \sim g(s_2)\)
Exercise 1-106(2)
Given a function \(\{1 \mapsto 12, 2 \mapsto 12, 3 \mapsto 3, 4 \mapsto 4\}\) from the four element set \(S\) to the three element set \(T\)
Choose a nontrivial partition \(c \in Prt(S)\) and compute \(g_!(c) \in Prt(T)\)
Choose any coarser partition \(g_!(c)\leq d \in Prt(T)\)
Choose any non-coarser partition \(g_!(c) > e \in Prt(T)\)
Find \(g^*(d)\) and \(g^*(e)\)
Show that the adjunction formula is true, i.e. that \(c \leq g^*(d)\) (because \(g_!(c) \leq d\)) and \(g^*(e) > c\) (because \(e > g_!(c)\))
Solution(1)
\(c = \{(1, 3),(2,), (4,)\}\), \(g_!(c)\) is then \(\{(12,3),(4,)\}\)
\(d = \{(12,),(3,),(4,)\}\)
\(e = \{(12,3,4)\}\)
\(g^*(d)=\{(1,2),(3,),(4,)\}, g^*(e)=\{(1,2,3,4)\}\)
\(c \leq g^*(d)\) and \(g^*(e) > c\)
Basic theory of Galois connections(12)
Galois connection alternate form(2)
Suppose \(P \overset{g}{\underset{f}{\leftrightarrows}} Q\) are monotone maps. The following are equivalent:
f and g form a Galois connection where f is left adjoint to g
for every \(p \in P, q \in Q\) we have:
\(p \leq g(f(p))\)
\(f(g(q)) \leq q\)
Proof(1)
Forward direction
Take any \(p \in P\) and let \(q = f(p) \in Q\)
By reflexivity, we have in \(Q\) that \(f(p) \leq q\)
By definition of Galois connection, we then have \(p \leq g(q)\), so (1) holds.
Take any \(q \in Q\) and let \(p = g(q) \in P\)
By reflexivity, we have in \(P\) that \(p \leq g(q)\)
By definition of Galois connection, we then have \(f(p) \leq q\), so (2) holds.
Reverse direction
Want to show \(f(p)\leq q \iff p \leq g(q)\)
Suppose \(f(p) \leq q\)
Since g is monotonic, \(g(f(p)) \leq g(q)\)
but, because (1), \(p \leq g(f(p))\), therefore \(p \leq g(q)\)
Suppose \(p \leq g(q)\)
Since f is monotonic, \(f(p) \leq f(g(q))\)
but, because (2), \(f(g(q)) \leq q\), therefore \(f(p) \leq q\)
Linked by
Adjoints preserving meets and joins(2)
Let \(P \overset{f}{\underset{g}{\rightleftarrows}} Q\) be monotone maps with \(f \dashv g\).
Right adjoints preserve meets
Left adjoints preserve joins
Given \(A \subseteq P\) and its image \(f(A) \subseteq Q\)
Then, if \(A\) has a join \(\vee A \in P\), then \(\vee f(a) \in Q\) exists
And \(f(\vee A) \cong \vee f(A)\)
Proof(1)
Left adjoints preserve joins
let \(j = \vee A \subseteq P\)
Given f is monotone, \(\forall a \in A: f(a) \leq f(j)\), i.e. we have \(f(a)\) as an upper bound for \(f(A)\)
To show it is a least upper bound, take some arbitrary other upper bound b for \(f(A)\) and show that \(f(j) \leq b\)
Because \(j\) is the least upper bound of \(A\), we have \(j \leq g(b)\)
Using the Galois connection, we have \(f(j) \leq b\) showing that \(f(j)\) is the least upper bound of \(f(A) \subseteq Q\).
Right adjoints preserving meets is dual to this.
Linked by
Adjoint functor theorem for preorders(2)
Adjoint functor theorem for preorders
Suppose \(Q\) is a preorder that has all meets and \(P\) is any preorder.
A monotone map \(Q \xrightarrow{g} P\) preserves meets iff it is a right adjoint.
Likewise, suppose \(P\) has all joins and \(Q\) is any preorder:
A monotone map \(P \xrightarrow{f} Q\) preserves joins iff it is a left adjoint.
Proved the reverse direction in Proposition 1.91.
Proof(1)
Given a right adjoint, construct the left adjoint by:
\(f(p) := \bigwedge\{q \in Q\ |\ p \leq g(q)\}\)
First need to show this is monotone:
If \(p \leq p'\), the relationship between the joined sets of \(f(p)\) and \(f(p')\) is that the latter is a subset of the former.
By Proposition 1.91 we infer that \(f(p) \leq f(p')\).
Then need to show that it is satisfies the left adjoint property:
Show that \(p_0 \leq g(f(p_0))\)
\(p_0 \leq \bigwedge \{g(q)\ |\ p_0 \leq g(q)\} \cong g(\bigwedge\{q\ |\ p_0 \leq g(q)\}) = g(f(p_0))\)
The first inequality comes from the fact that the meet of the set (of which \(p_0\) is a lower bound) is a greatest lower bound.
The congruence comes from the fact that right adjoints preserve meets.
Show that \(f(g(q_0)) \leq q_0\)
\(f(g(q_0)) = \bigwedge\{q\ |\ g(q_0) \leq g(q)\} \leq \bigwedge \{q_0\} = q_0\)
The first inequality comes from Proposition 1.91 since \(\{q_0\}\) is a subset of the first set.
The second equality is a property of the meet of single element sets.
Proof of a left adjoint construction (assuming it preserves joins) is dual.
Linked by
Adjoints in Set(1)
Let \(A \xrightarrow{f} B\) be a set function, say between apples and buckets into which we put each apple.
The ‘pullback along f’ \(\mathbb{P}(B) \xrightarrow{f^*} \mathbb{P}(A)\) maps each subset \(B' \subseteq B\) to its preimage \(f^{-1}(B') \subseteq A\)
It tells you for a set of buckets all the apples contained in total.
It is a monotonic map which has a left and right adjoint: \(f_! \dashv f^* \dashv f_*\)
The left adjoint \(\mathbb{P}(A)\xrightarrow{f_!}\mathbb{P}(B)\) is given by the direct image
\(f_!(A') := \{b \in B\ |\ \exists a \in A': f(a)=b\}\)
Tells you for a set of apples all the buckets that contain at least one of those apples.
The right adjoint \(\mathbb{P}(A) \xrightarrow{f_*} \mathbb{P}(B)\) is defined as follows:
\(f_*(A') := \{b \in B\ |\ \forall a: f(a)=b \implies a \in A'\}\)
Tells you all the buckets which are all-\(A\prime\) (note that empty buckets vacuously satisfy this condition).
Adjoints often turn out to have interesting semantic interpretations.
If we replace the \(\leq\) in Proposition 1.107 with \(=\), then we obtain the notion of a preorder isomorphism.
Since left adjoints preserve joins, we know a monotone map cannot have generative effects iff it is left adjoint to some other monotone.
Exercise 1-110(2)
Show that if \(P \xrightarrow{f}Q\) has a right adjoint g, then it is unique up to isomorphism. Is the same true for left adjoints?
Solution(1)
Suppose \(h\) is also right adjoint to \(f\).
What it means for \(h \cong g\):
\(\forall q \in Q: h(q) \cong g(q)\)
\(g(q) \leq h(q)\)
Substitute \(g(q)\) for \(p\) in \(p \leq h(f(p))\) (from \(h\)’s adjointness) to get \(g(q) \leq h(f(g(q)))\)
Also apply \(h\) to both sides of \(f(g(q)) \leq q\) (from \(g\)’s adjointness) to get \(h(f(g(q)))\leq h(q)\)
The result follows from transitivity.
By symmetry (nothing was specified about \(h\) or \(g\)) the proof of \(h(q)\leq g(q)\) is the same.
Same reasoning for left adjoints.
Exercise 1-118(2)
Choose sets \(X,Y\) with between two and four elements each, and choose a function \(X \xrightarrow{f} Y\) NOCARD
Choose two different subsets \(B_1, B_2 \subseteq Y\) and find \(f^*(B_1)\) and \(f^*(B_2)\)
Choose two different subsets \(A_1, A_2 \subseteq X\) and find \(f_!(A_1)\) and \(f_!(A_2)\)
With the same \(A_1, A_2\) find \(f_*(A_1)\) and \(f_*(A_2)\)
Solution(1)
\(\bar 3 \xrightarrow{f} \bar 4\) with \(\{1 \mapsto 2, 2 \mapsto 2, 3\mapsto 4\}\),\(A_1 = \{1,2\}, A_2=\{2,3\}, B_1=\{1\}, B_2=\{1,4\}\)
\(f^*(B_1)=\varnothing, f^*(B_2)=\{4\}\)
\(f_!(A_1)=\{2\},f_!(A_2)=\{2,4\}\)
\(f_*(A_1)=\{1,2,3\},f_*(A_2)=\{1,3,4\}\)
Closure operators(7)
Given a Galois connection we can compose the left and right maps to get a closure operator
Closure operator(1)
A closure operator \(P \xrightarrow{j} P\) on a preorder \(P\)
A monotone map such that for all \(p \in P\) we have:
\(p \leq j(p)\)
\(j(j(p)) \cong j(p)\)
Linked by
Eval as closure(1)
Example of a closure operator
Think of the preorder of arithmatic expressions such as \(12, 4+2+4, 9*(2+3)\), where the \(\leq\) operators denotes whether an expression can be simplified to another.
A computer program \(j\) that evaluates expressions is a monotonic function on the preorder to itself (if you can reduce x to y, then \(j(x)\) should be able to be rewritten as \(j(y)\).
The requirements of closure operator say that \(j\) should be a simplification, and that trying to reduce an expression which has already been reduced will do nothing further.
Adjunctions from closures(1)
Just as adjunctions give rise to closure operators, from every closure operator we may construct an adjunction.
Let \(P \xrightarrow{j} P\) be a closure operator.
Get a new preorder by looking at a subset of \(P\) fixed by \(j\).
\(fix_j\) defined as \(\{p \in P\ |\ j(p)\cong p\}\)
Define a left adjoint \(P \xrightarrow{j} fix_j\) and right adjoint \(fix_j \xhookrightarrow{g} P\) as simply the inclusion function.
To see that \(j \dashv g\), we need to verify \(j(p) \leq q \iff p \leq q\)
Show \(\rightarrow\):
Because \(j\) is a closure operator, \(p \leq j(p)\)
\(j(p) \leq q\) implies \(p \leq q\) by transivity.
Show \(\leftarrow\):
By monotonicity of \(j\) we have \(p \leq q\) implying \(j(p) \leq j(q)\)
\(q\) is a fix point, so the RHS is congruent to \(q\), giving \(j(p) \leq q\).
Closures in logic(1)
Examples of closure operators from logic.
Take set of all propositions as a preorder, where \(p \leq q\) iff \(p\) implies \(q\).
Some modal operators are closure operators
E.g. \(j(p)\) means “Assuming Bob is in Chicago, p”
\(p \implies j(p)\) (the logic is monotonic, adding assumptions does not make something true into something false.
\(j(j(p)) = j(p)\) (the assumption is idempotent)
Exercise 1-119(2)
Given \(f \dashv g\), prove that the composition of left and right adjoint monotone maps is a closure operator
Show \(p \leq (f;g)(p)\)
Show \((f;g;f;g)(p) \cong (f;g)(p)\)
Solution(1)
This is one of the conditions of adjoint functors: \(p \leq g(f(p))\)
The \(\leq\) direction is an extension of the above: \(p \leq g(f(p)) \leq g(f(g(f(p))))\)
Galois property: \(q \geq f(g(q))\), substitute \(f(p)\) for \(q\) to get \(f(p) \geq f(g(f(p)))\).
Because \(g\) is a monotone map, we can apply it to both sides to get \(g(f(p)) \geq g(f(g(f(p))))\)
Level shifting(3)
Preorder of relations(1)
‘Level shifting’
Given any set \(S\), there is a set \(\mathbf{Rel}(S)\) of binary relations on \(S\) (i.e. \(\mathbb{P}(S \times S)\))
This power set can be given a preorder structure using the subset relation.
A subset of possible relations satisfy the axioms of preorder relations. \(\mathbf{Pos}(S) \subseteq \mathbb{P}(S \times S)\) which again inherits a preorder structure from the subset relation
A preorder on the possible preorder structures of \(S\), that’s a level shift.
The inclusion map \(\mathbf{Pos}(S) \hookrightarrow \mathbf{Rel}(S)\) is a right adjoint to a Galois connection, while its left adjoint is \(\mathbf{Rel}(S)\overset{Cl}{\twoheadrightarrow} \mathbf{Pos}(S)\) which takes the reflexive and transitive closure of an arbitrary relation.
Exercise 1-125(2)
Let \(S=\{1,2,3\}\)
Come up with any preorder relation on \(S\), and define \(U(\leq):=\{(s_1,s_2)\ |\ s_1 \leq s_2\}\) (the relation ‘underlying’ the preorder. Note \(\mathbf{Pos}(S) \xhookrightarrow{U} \mathbf{Rel}(S)\))
Pick binary relations such that \(Q \subseteq U(\leq)\) and \(Q' \not \subseteq U(\leq)\)
We want to check that the reflexive/transitive closure operation \(Cl\) is really left adjoint to the underlying relation \(U\).
The meaning of \(Cl \dashv U\) is \(Cl(R) \sqsubset \leq \iff R \sqsubset U(\leq)\), where \(\sqsubset\) is the order relation on \(\mathbf{Pos}(S)\)
Concretely show that \(Cl(Q) \sqsubset \leq\)
Concretely show that \(Cl(Q') \not \sqsubset \leq\)
Solution(1)
Let the preorder be given by this diagram (with implicit reflexive arrows):
Let \(Q\) be given by the following diagram
and let \(Q'=S\times S\)
\(Cl(Q) = \{11,12,22,33\}\) \(\sqsubset\) \(\leq = \{11,22,33,12,23,13\}\)
\(Cl(Q') = Q' = S \times S\) \(\not \sqsubset\) \(\leq\) (reason: \((3,1) \in S \times S\) but \((3,1) \not \in \leq\))
Chapter 2: Resource theories(112)
Getting from A to B(1)
Want to be able to answer questions about resources like:
Given what I have, is it possible to get what I want?
Given what I have, what is the minimum cost to get what I want?
Given what I have, what is the set of ways to get what I want?
Monoidal preorders will allow us to build new recipes from old ones.
Resources are not always consumed when used.
A \(\mathcal{V}\) category is a set of objects, which one may think of as points on a map
\(\mathcal{V}\) somehow ’structures the question’ of getting from point a to b
\(\mathcal{V} = Bool\) answers the question of whether we can get to b
\(\mathcal{V} = Cost\) can help answer how to get to b with minimum cost.
\(\mathcal{V} = \mathbf{Set}\) can yield a set of methods to get to b.
Symmetric monoidal preorders(40)
Definition and first examples(9)
The notation for monoidal product and unit may vary depending on context. \(I, \otimes\) are defaults but it may be best to use \((0,+),(1,*),(true, \land)\) (etc.)
Symmetric monoidal structure on a preorder(1)
A symmetric monoidal structure on a preorder \((X, \leq)\)
Two additional constituents:
A monoidal unit \(I \in X\)
A monoidal product \(X \times X \xrightarrow{\otimes} X\)
Satisfying the following properties:
Monotonicity: \(\forall x_1,x_2,y_1,y_2 \in X: x_1 \leq y_1 \land x_2 \leq y_2 \implies x_1 \otimes x_2 \leq y_1 \otimes y_2\)
Unitality: \(\forall x \in X: I \otimes x = x = x \otimes I\)
Associativity: \(\forall x,y,z \in X: (x \otimes y) \otimes z = x \otimes (y\otimes z)\)
Symmetry: \(\forall x,y \in X: x \otimes y = y \otimes x\)
Linked by
- Weak monoidal structure on a preorder: referenced
- Discrete SMP: referenced
- Exercise 2-5: referenced
- Exercise 2-8: referenced
- Introducing wiring diagrams: referenced
- Exercise 2-20: referenced
- Abstract examples: referenced
- Opposite SMP: referenced
- Natural numbers SMP: referenced
- Natural numbers SMP: referenced
- Divisibility SMP: referenced
- Divisibility SMP: referenced
- Cost SMP: referenced
- Exercise 2-31: referenced
- Exercise 2-33: referenced
- Exercise 2-34: referenced
- Exercise 2-34: referenced
- Exercise 2-35: referenced
- Exercise 2-45: referenced
- Exercise 2-45: referenced
- V-category: referenced
- Lawvere metric space: referenced
- Exercise 2-55: referenced
- Exercise 2-61: referenced
- Exercise 2-62: referenced
- Exercise 2-63: referenced
- Closed SMP: referenced
- Cost is closed: referenced
- Chemistry closed resource theory: referenced
- Exercise 2-82: referenced
- Exercise 2-82: referenced
- Solution: referenced
- Quantale is SMP with all joins: referenced
- Exercise 2-94: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Monoidal categories: referenced
- Monoidal categories: referenced
Weak monoidal structure on a preorder(1)
A weak monoidal structure on a preorder \((X, \leq)\)
Definition is identical to a symmetric monoidal structure, replacing all \(=\) signs with \(\cong\) signs.
Discrete SMP(1)
A monoid is a set \(M\) with a monoid unit \(e \in M\) and associative monoid multiplication \(M \times M \xrightarrow{\star} M\) such that \(m \star e=m=e \star m\)
Every set \(S\) determines a discrete preorder: \(\mathbf{Disc}_S\)
It is easy to check if \((M,e,\star)\) is a commutative monoid then \((\mathbf{Disc}_M, =, e, \star)\) is a symmetric monoidal preorder.
Linked by
Poker hands(1)
Let \(H\) be the set of all poker hands, ordered by \(h \leq h'\) if \(h'\) beats or ties hand \(h\).
One can propose a monoidal product by assigning \(h_1 \otimes h_2\) to be “the best hand one can form out of the ten cards in \(h_1 \bigcup h_2\)"
This proposal will fail monotonicity with the following example:
\(h_1 := \{2\heartsuit, 3\heartsuit,10 \spadesuit,J\spadesuit,Q\spadesuit\} \leq i_1 := \{4\spadesuit,4\spadesuit,6\heartsuit,6\diamondsuit,10\diamondsuit\}\)
\(h_2 := \{2\diamondsuit,3\diamondsuit,4\diamondsuit,K\spadesuit,A\spadesuit\} \leq i_2 := \{5\spadesuit,5\heartsuit,7\heartsuit,J\diamondsuit,Q\diamondsuit\}\)
\(h_1 \otimes h_2=\{10\spadesuit,J\spadesuit,Q\spadesuit,K\spadesuit,A\spadesuit\} \not \leq i_2 \otimes i_2 = \{5\spadesuit, 5\heartsuit,6\heartsuit,6\diamondsuit,Q\diamondsuit\}\)
Exercise 2-5(2)
Consider the reals ordered by our normal \(\leq\) relation. Do \((1,*)\) as unit and product for a symmetric monoidal structure?
Solution(1)
No, monotonicity fails: \(x_1\leq y_1 \land x_2 \leq y_2 \not \implies x_1x_2 \leq y_1y_2\) (Counterexample: \(x_1=x_2=-1, y_1=y_2=0\))
Exercise 2-8(2)
Check if \((M,e,\star)\) is a commutative monoid then \((\mathbf{Disc}_M, =, e, \star)\) is a symmetric monoidal preorder, as described in this example.
Solution(1)
Monotonicity is the only tricky one, and is addressed due to the triviality of the discrete preorder.
We can replace \(x \leq y\) with \(x \leq x\) because it is a discrete preorder.
\(x_1 \leq x_1 \land x_2 \leq x_2 \implies x_1 \otimes x_2 \leq x_1 \otimes x_2\)
\(True \land True \implies True\) is vacuously true due to reflexivity of preorder.
Unitality/associativity comes from unitality/associativity of monoid
Symmetry comes from commutitivity of monoid.
Introducing wiring diagrams(3)
Exercise 2-20(2)
Given the assertions the interior of this wiring diagram:
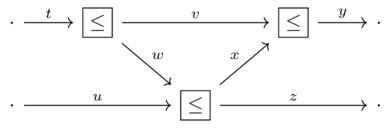
Prove that the conclusion follows using the rules of symmetric monoidal preorders
Make sure to use reflexivity and transitivity
How do you know that symmetry axiom does not need to be invoked?
Solution(1)
Assertions:
\(t \leq v+w\)
\(w+u \leq x+z\)
\(v+x \leq y\)
Conclusion: \(t+u \leq y+z\)
Proof:
\((t)+(u) \leq (v+w)+(u)\) - from monotonicity and reflexivity of u
\(= v+(w+u)\) - associativity
\(\leq v+(x+z)\) - monotonicity and reflexivity of v
\(= (v+x)+z\) - associativity
\(\leq y+z\) - monotonicity and reflexivity of z
Symmetry was not needed because the diagram had no crossing wires.
Visual representations for building new relationships from old.
For a preorder without a monoidal structure, we can only chain relationships linearly (due to transitivity).
For a symmetric monoidal structure, we can combine relationships in series and in parallel.
Call boxes and wires icons
Any element \(x \in X\) can be a label for a wire. Given x and y, we can write them as two wires in parallel or one wire \(x \otimes y\); these are two ways of representing the same thing.
Consider a wire labeled \(I\) to be equivalent to the absence of a wire.
Given a \(\leq\) block, we say a wiring diagram is valid if the monoidal product of elements on the left is less than those on the right.
Let’s consider the properties of the order structure:
Reflexivity: a diagram consisting of just one wire is always valid.
Transitivity: diagrams can be connected together if outputs = inputs
Monotonicity: Stacking two valid boxes in parallel is still valid.
Unitality: We need not worry about \(I\) or blank space
Associativity: Need not worry about building diagrams from top-to-bottom or vice-versa.
Symmetry: A diaagram is valid even if its wires cross.
One may regard crossing wires as another icon in the iconography.
Wiring diagrams can be thought of as graphical proofs
If subdiagrams are true, then the outer diagram is true.
Applied examples(1)
Resource theories:
As discussed here, we consider ’static’ notions.
Chemistry: reactants + catalyst \(<\) products + catalyst
Manufacturing: you can trash anything you want, and it disappears from view (requires \(\forall x: x \leq I\))
Informatics: in addition to trashing, information can be copied (requires \(x \leq x + x\))
Abstract examples(18)
Booleans important for the notion of enrichment.
Enriching in a symmetric monoidal preorder \(\mathcal{V}=(V,\leq,I,\otimes)\) means "letting \(\mathcal{V}\) structure the question of getting from a to b"
Consider \(\mathbf{Bool}=(\mathbb{B},\leq,true,\land)\)
The fact that the underlying set is \(\{false, true\}\) means that “getting from a to b is a true/false question"
The fact that \(true\) is the monoidal unit translates to the saying “you can always get from a to a"
The fact that \(\land\) is the moniodal product means “if you can get from a to b and b to c then you can get from a to c"
The ‘if ... then ...’ form of the previous sentence is coming from the order relation \(\leq\).
Opposite SMP(2)
The opposite of a symmetric monoidal preorder \((X, \geq, I, \otimes)\) is still a symmetric monoidal preorder
Proof(1)
Monotonicity: \(x_1 \geq y_1 \land x_2 \geq y_2 \implies x_1 \otimes x_2 \geq y_1 \otimes y_2\)
This holds because monotonicity holds in the original preorder (\(a\geq b \equiv b \leq a\)).
Unitality, symmetry, and associativity are not affected by the preorder.
Natural numbers SMP(1)
There is a symmetric monoidal structure on \((\mathbb{N}, \leq)\) where the monoidal unit is zero and the product is \(+\) (\(6+4=10\)). Monotonicity (\((x_1,x_2)\leq(y_1,y_2) \implies x_1+x_2 \leq y_1+y_2\)) and other conditions hold.
Divisibility SMP(1)
Recall the divisibility order \((\mathbb{N}, |)\)
There is a symmetric monoidal structure on this preorder with unit \(1\) and product \(*\).
Monotonicity (\(x_1|y_1 \land x_2|y_2 \implies x_1*x_2 | y_1*y_2\)) and other conditions hold.
Cost SMP(1)
Lawvere’s symmetric monoidal preorder, Cost.
Let \([0,\infty]\) represent the non-negative real numbers with infinity. Also take the usual notion of \(\geq\).
There is a monoidal structure for this preorder: \(\mathbf{Cost}:=([0,\infty],\geq,0,+)\)
The monoidal unit being zero means “you can get from a to a at no cost."
The product being + means “getting from a to c is at most the cost of a to b plus b to c"
The ‘at most’ above comes from the \(\geq\).
Linked by
Exercise 2-31(2)
Show there is a symmetric monoidal structure on \((\mathbb{N}, \leq)\) where the monoidal product is \(6*4=24\). What should the monoidal unit be?
Solution(1)
Let the monoidal product be the standard product for integers, with 1 as unit.
Monotonicity: \((x_1,x_2)\leq (y_1,y_2) \implies x_1x_2 \leq y_1y_2\)
Unitality: \(1*x_1=x_1=x_1*1\)
Associativity: \(a*(b*c)=(a*b)*c\)
Symmetry: \(a*b=b*a\)
Exercise 2-33(2)
Recall the divisibility order \((\mathbb{N}, |)\). Someone proposes \((0,+)\) as the monoidal unit and product. Does this satisfy the conditions of a symmetric monoidal structure?
Solution(1)
Conditions 2-4 are satisfied, but not monotonicity: \(1|1 \land 2|4\) but not \(3 | 5\)
Exercise 2-34(2)
Consider the preorder defined by the Hasse diagram \(\boxed{no \rightarrow maybe \rightarrow yes}\)
Consider a potential monoidal structure with \(yes\) as the unit and \(min\) as the product.
Fill out a reasonable definition of \(min\) and check that it satisfies the conditions.
Solution(1)
| \(min\) | no | maybe | yes |
|---|---|---|---|
| no | no | no | no |
| maybe | no | maybe | maybe |
| yes | no | maybe | yes |
Monotonicity: \(x_1 \leq y_1 \land x_2 \leq y_2 \implies x_1x_2 \leq y_1y_2\)
Suppose without loss of generality that \(x_1\leq x_2\)
then \(x_1x_2=x_1\) and \(y_1y_2 = y_1\) or \(y_2\)
In the first case, we know this is true because we assumed \(x_1 \leq y_1\)
In the second case, we know it from transitivity: \(x_1 \leq x_2\leq y_2\)
Unitality: \(min(x,yes)=x\)
Associativity: probably
Symmetry: table is symmetric.
Linked by
Exercise 2-35(2)
Check that there is a symmetric monoidal structure on the power set of \(S\) ordered by subset relation. (The unit is \(S\) and product is \(\cap\))
Solution(1)
Monotonicity: \(x_1 \subseteq y_1 \land x_2 \subseteq y_2 \implies x_1 \cap x_2 \subseteq y_1 \cap y_2\)
This is true: if something is in both \(x_1,x_2\), then it is in both \(y_1,y_2\), i.e. in their intersection.
Unitality: \(x \cap S = x = S \cap x\), since \(\forall x \in P(S): x \subseteq S\).
Associativity and symmetry come from associativity and symmetry of \(\cap\) operator.
Exercise 2-36(2)
Let \(Prop^\mathbb{N}\) be the set of all mathematical statements one can make about a natural number.
Examples:
n is a prime
n = 2
\(n \geq 11\)
We say \(P \leq Q\) if for all \(n \in \mathbb{N}\), \(P(n) \implies Q(n)\)
Define a monoidal unit and product on \((Prop^\mathbb{N}, \leq)\).
Solution(1)
Let the unit be \(\lambda x. true\) and product be \(\land\)
montonicity: \(P_1(x)\leq Q_1(x) \land P_2(x) \leq Q_2(x) \implies (P_1 \land P_2)(x) \leq (Q_1 \land Q_2)(x)\)
If the \(P\) properties hold for a given number, then each of the \(Q\) properties hold
unitality, associativity, symmetry: same as \(\mathbf{Bool}\)
Exercise 2-40(2)
Consider \(\mathbf{Cost}^{op}\). What is it as a preorder? What is its unit and product?
Solution(1)
As a preorder, the domain is still \([0,\infty]\) and ordered by the natural \(\leq\) relation. The unit and product are unchanged by taking the opposite preorder, so they are still \(0, +\) respectively.
Monoidal monotone maps(9)
Monoidal montones are examples of monoidal functors, specifically lax ones. Oplax functors are a dual notion which has the inequalities reversed.
Monoidal monotone(1)
A monoidal monotone map from \((P,\leq_P,I_P,\otimes_P)\) to \((Q, \leq_Q,I_Q,\otimes_Q)\). Also, a strong monoidal monotone map and a strict monoidal monotone map
A monotone map \((P,\leq_P) \xrightarrow{f} (Q,\leq_Q)\) satsifying two conditions:
\(I_Q \leq_Q f(I_P)\)
\(\forall p_1,p_2 \in P:\) \(f(p_1)\ \otimes_Q\ f(p_2)\ \leq_Q\ f(p_1\ \otimes_P\ p_2)\)
If the \(\leq\) are replaced with \(\cong\), the map is strong, and if replaced with \(=\), it is strict.
Linked by
- Natural Real monoidal monotones: referenced
- Exercise 2-43: referenced
- Exercise 2-43: referenced
- Solution: referenced
- Exercise 2-44: referenced
- Exercise 2-45: referenced
- Solution: referenced
- Induced V-categories from monoidal monotones: referenced
- Proof: referenced
- Proof: referenced
- Metric space to preorder: referenced
- Exercise 2-67: referenced
- Exercise 2-68: referenced
- Solution: referenced
Natural Real monoidal monotones(1)
Strict monoidal monotone injection \((\mathbb{N},\leq, 0, +) \xhookrightarrow{i} (\mathbb{R},\leq,0,+)\)
There is also a monoidal monotone \((\mathbb{R}^+,\leq, 0, +) \xrightarrow{\lfloor x \rfloor} (\mathbb{N},\leq,0,+)\)
Monotonic: \(x \leq_\mathbb{R} y \implies \lfloor x \rfloor \leq \lfloor y \rfloor\)
But it is neither strict nor strong: \(\lfloor 0.5 \rfloor + \lfloor 0.5 \rfloor \not \cong \lfloor 0.5+0.5 \rfloor\)
Exercise 2-43(2)
Consider a proposed monoidal monotone \(\mathbf{Bool}\xrightarrow{g}\mathbf{Cost}\) with \(g(false)=\infty, g(true)=0\)
Check that the map is monotonic and that it satisfies both properties of monoidal monotones.
Is g strict?
Solution(1)
It is monotonic: \(\forall a,b \in \mathbb{B}: a\leq b \implies g(a)\leq g(b)\)
there is only one nonidentity case in \(\mathbf{Bool}\) to cover, and it is true that \(\infty\ \leq_\mathbf{Cost}\ 0\).
Condition on units: \(0 \leq_\mathbf{Cost} g(true)\) (actually, it is equal)
In \(\mathbf{Cost}\): \(g(x) + g(y) \geq g(x \land y)\)
if both true/false, the equality condition holds.
If one is true and one is false, then LHS and RHS are \(\infty\) (as \(x \land y = False\)).
Therefore this is a strict monoidal monotone.
Exercise 2-44(2)
Consider the following functions \(\mathbf{Cost} \xrightarrow{d,u} \mathbf{Bool}\)
\(d(x>0)\mapsto false,\ d(0)\mapsto true\)
\(u(x=\infty)\mapsto false,\ d(x < \infty) \mapsto true\)
For both of these, answer:
Is it monotonic?
If so, does it satsify the monoidal monotone properties?
If so, is it strict?
Solution(1)
The function \(d\) asks “Is it zero?”, and the function \(u\) asks “Is it finite?”.
Both of these questions are monotone: as we traverse forward in \(\leq_{Cost}\), we traverse towards being zero or being finite.
The first monoidal monotone axiom is satisifed in both because the unit (\(0\)) is mapped to the unit (\(True\)).
The second monoidal monotone axiom holds for both because addition preserves both things being zero (or not) and both things being finite (or not).
These are strict because, in \(Bool\), equality and congruence coincide.
Linked by
Exercise 2-45(2)
Is \((\mathbb{N},\leq,1,*)\) a symmetric monoidal preorder?
If so, does there exist a monoidal monotone \((\mathbb{N},\leq,0,+) \rightarrow (\mathbb{N},\leq,1,*)\)
Is \((\mathbb{Z},\leq,*,1)\) a symmetric monoidal preorder?
Solution(1)
Yes. Monotonicity holds, and multiplication by 1 is unital. The operator is symmetric and associative.
Exponentiation (say, by \(2\)) is a strict monoidal monotone.
\(1 = 2^0\) and \(2^x * 2^y = 2^{x+y}\)
No: monotonicity does not hold (multiplying negative numbers gives a larger number).
Enrichment(20)
V-categories(2)
V-category(1)
A \(\mathcal{V}\) category, given a symmetric monoidal preorder \(\mathcal{V}=(V,\leq,I,\otimes)\)
To specify the category \(\mathcal{X}\), one specifies:
A set \(Ob(\mathcal{X})\) whose elements are called objects
A hom-object for every pair of objects in \(Ob(\mathcal{X})\), written \(\mathcal{X}(x,y) \in V\)
The following properties must be satisfied:
\(\forall x \in Ob(\mathcal{X}):\) \(I \leq \mathcal{X}(x,x)\)
\(\forall x,y,z \in Ob(\mathcal{X}):\) \(\mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)
We call \(\mathcal{V}\) the base of enrichment for \(\mathcal{X}\) or say that \(\mathcal{X}\) is enriched in \(\mathcal{V}\).
Linked by
- Getting from A to B: referenced
- Bool-category: referenced
- Bool-category: referenced
- Preorders are Bool-categories: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Lawvere metric space: referenced
- Lawvere metric space: referenced
- Lawvere metric space: referenced
- Exercise 2-55: referenced
- Exercise 2-61: referenced
- Exercise 2-62: referenced
- Exercise 2-62: referenced
- Exercise 2-62: referenced
- Exercise 2-63: referenced
- Induced V-categories from monoidal monotones: referenced
- Induced V-categories from monoidal monotones: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- V-functor: referenced
- Bool-functors: referenced
- Exercise 2-73: referenced
- Exercise 2-73: referenced
- Exercise 2-73: referenced
- Exercise 2-73: referenced
- Solution: referenced
- Solution: referenced
- Solution: referenced
- V-category product: referenced
- V-category product: referenced
- Cost-category product: referenced
- Cost-category product: referenced
- Exercise 2-75: referenced
- Exercise 2-78: referenced
- Self-enriched category: referenced
- Self-enriched category: referenced
- Self-enriched category: referenced
- Feasibility relationships as Bool-profunctors: referenced
- V-profunctors: referenced
- V-profunctor: referenced
- Bool-profunctors: referenced
- The unit profunctor: referenced
- Proof: referenced
- Proof: referenced
- Exercise 4-26: referenced
- V-profunctor collage: referenced
- Monoidal categories: referenced
- Monoidal categories: referenced
- Categories enriched in a symmetric monoidal category: referenced
Bool-category(1)
Consider the following preorder:
As a Bool-category, the objects are \(Ob(\mathcal{X})=\{p,q,r,s,t\}\).
For every pair, we need an element of Bool, so make it true if \(x\leq y\)
\(true\) is the monoidal unit of Bool, and this obeys the two constraints of a \(\mathcal{V}\) category.
We can represent the binary relation (hom-object) with a table:
\(\leq\) p q r s t p T T T T T q F T F T T r F F T T T s F F F T T t F F F F T
Preorders as Bool-categories(2)
Preorders are Bool-categories(2)
There is a one-to-one correspondence between preorders and Bool-categories
Proof(1)
Construct preorder \((X,\leq_X)\) from any Bool-category \(\mathcal{X}\)
Let \(X\) be \(Ob(\mathcal{X})\) and \(x\ \leq_X\ y\) be defined as \(\mathcal{X}(x,y)=true\)
This is reflexive and transitive because of the two constraints we put on enriched categories.
The first constraint says that \(true \leq (x \leq_X x)\)
The second constraint says \((x \leq_X y) \land (y \leq_X z) \leq (x \leq_X z)\)
Construct Bool-category from a preorder:
Let \(Ob(X)=X\) and define \(\mathcal{X}(x,y)=true\) iff \(x \leq_X y\)
The two constraints on preorders give us our two required constraints on enriched categories.
Lawvere metric spaces(10)
Can convert any weighted graph into a Lawvere metric space, where a the distance is the sum of weights along the shortest path.
It can be hard to see the shortest path by inspection, but a matrix power iteration method (starting from just a matrix of edge weights) is possible.
Metric space(1)
A metric space \((X,d)\)
A set \(X\) whose elements are called points
A function \(X \times X \xrightarrow{d} \mathbb{R}_{\geq 0}\) which gives the distance between two points.
These must satisfy three properties:
\(d(x,y)=0 \iff x=y\)
\(d(x,y)=d(y,x)\)
\(d(x,y)+d(y,z)\geq d(x,z)\) (triangle inequality)
An extended metric space includes \(\infty\) in the codomain of the cost function.
Linked by
Lawvere metric space(1)
A Lawvere metric space
A Cost-category, i.e. a category enriched in the symmetric monoidal preorder \(\mathbf{Cost}=([0,\infty],\geq,0,+)\).
\(X\) is given as \(Ob(\mathcal{X})\)
\(d(x,y)\) is given as \(\mathcal{X}(x,y)\)
The axiomatic properties of a category enriched in Cost are:
\(0 \geq d(x,x)\)
\(d(x,y)+d(y,z) \geq d(x,z)\)
Linked by
Reals metric space(1)
The set \(\mathbb{R}\) can be given a metric space structure, with \(d(x,y)=|x-y|\).
Exercise 2-52(2)
Imagine the points of a metric space are whole regions, like US, Spain, and Boston. Distance is "Given the worst case scenario, how far do you have to travel to get from region A to B?"
This actually breaks our symmetry requirement: \(d(Boston,US)=0, d(US,Boston) > 0\)
Which distance is bigger in this framework: \(d(Spain,US)\) or \(d(US,Spain)\)?
Solution(1)
\(d(US,Spain)\) is bigger because there is much more room for the worst case scenario to place one farther for Spain.
A bigger first argument makes things strictly worse, all else equal. A bigger second argument makes things strictly better, all else equal.
Linked by
Exercise 2-55(2)
Consider the symmetric monoidal preorder \((\mathbb{R},\geq,0,+)\) which is the same as Cost but does not include \(\infty\). How do you characterize the difference between this and a Lawvere metric space in the sense of definition 2.46?
Solution(1)
It is a metric space in which points may only be finitely-far apart.
Exercise 2-60(2)
What is the distance matrix represented by this graph?
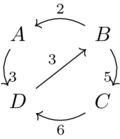
Solution(1)
| \(\rightarrow\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 6 | 3 | 11 |
| B | 2 | 0 | 5 | 5 |
| C | 5 | 3 | 0 | 8 |
| D | 11 | 9 | 6 | 0 |
Linked by
V-variations on preorders and metric spaces(6)
Exercise 2-61(2)
Recall the symmetric monoidal preorder \(\mathbf{NMY} := (P,\leq, yes, min)\) from Exercise 2.34. Interpret what a NMY-category is.
Solution(1)
It is like a graph where some edges are ‘maybe’ edges. We can ask the question “Is there a path from a to b?" and if there is a true path we will get a ‘yes’. If the only paths are those which include maybe edges, then we get a ’maybe’. If there’s no path at all, we get a ‘no’.
Exercise 2-62(2)
Let \(M\) be a set and \(\mathcal{M}:=(P(M),\subseteq, M, \cap)\) be the symmetric monoidal preorder whose elements are subsets of \(M\).
Someone says "for any set \(M\), imagine it as the set of modes of transportation (e.g. car, boat, foot)". Then an \(\mathcal{M}\) category \(\mathcal{X}\) tells you all the modes that will get you from a all the way to b, for any two points \(a,b \in Ob(\mathcal{X})\)
Draw a graph with four vertices and five edges, labeled with a subset of \(M=\{car,boat,foot\}\)
From this graph it is possible to construct an \(\mathcal{M}\) category where the hom-object from x to y is the union of the sets for each path from x to y, where the set of a path is the intersection of the sets along the path. Write out the corresponding 4x4 matrix of hom-objects and convince yourself this is indeed an \(\mathcal{M}\) category.
Does the person’s interpretation look right?
Solution(1)
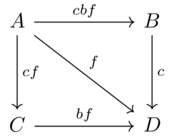
(implicitly, no path means edge of \(\varnothing\) and self paths are \(cfb\))
Hom objects:
A B C D A cbf cbf cf cf B \(\varnothing\) cbf \(\varnothing\) c C \(\varnothing\) \(\varnothing\) cbf bf D \(\varnothing\) \(\varnothing\) \(\varnothing\) cbf The first property (\(\forall x \in Ob(\mathcal{X}): I \leq \mathcal{X}(x,x)\)) is satisfied by noting the diagonal entries are equal to the unit.
The second property (\(\forall x,y,z \in Ob(\mathcal{X}): \mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)) can be checked looking at the following cases:
\(A \rightarrow B \rightarrow D\): \(cbf \cap c \leq cf\)
\(A \rightarrow C \rightarrow D\): \(cf \cap bf \leq cf\)
One subtlety is that we need to say that one can get from any place to itself by any means of transportation for this to make sense. Overall interpretation looks good.
Exercise 2-63(2)
Consider the symmetric monoidal preorder \(\mathcal{W}:=(\mathbb{N}\cup\{\infty\},\leq,\infty,min)\)
Draw a small graph labeled by elements of \(\mathbb{N}\cup\{\infty\}\)
Write a the matrix whose rows and columns are indexed by nodes in the graph, whose (x,y)th entry is given by the maximum over all paths p from x to y of the minimum edge label in p.
Prove that this matrix is a matrix of hom-objects for a \(\mathcal{W}\) category called \(\mathcal{X}\).
Make up an interpretation for what it means to enrich in \(\mathcal{W}\)
Solution(1)
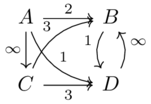
(implicitly, no path means path of weight 0, and self paths have weight \(\infty\))
Maxmin matrix:
A B C D A \(\infty\) 3 \(\infty\) 3 B 0 \(\infty\) 0 \(\infty\) C 0 3 \(\infty\) 3 D 0 1 0 \(\infty\) Self paths are equal to the monoidal unit and it will never be the case that \(min(\mathcal{X}(A,B),\mathcal{X}(B,C)) > \mathcal{X}(A,C)\) because even in the worst-case scenario (where there is not a better path from A to C that ignores B completely), we form the best path by combining the best path from A to B with the best from B to C. We are forced to take the minimum edge label in the path, which means that the lowest \(\mathcal{X}(A,C)\) can be is actually equal to the left hand side.
The edges could represent constraints (\(\infty\) is fully unconstrained, \(0\) is fully constrained, e.g. the diameter of a pipe) and the hom-object represents the least-constrained thing that can get from one point to another. The monoidal unit says that something can be fully unconstrained if it stays where it is, and the monoidal product (min) says how to compose two different constraints in series.
Constructions on V-categories(18)
Changing the base of enrichment(7)
Induced V-categories from monoidal monotones(2)
Let \(\mathcal{V}\xrightarrow{f}\mathcal{W}\) be a monoidal monotone map. Given a \(\mathcal{V}\) category, called \(\mathcal{C}\), one can construct an associated \(\mathcal{W}\) category, let’s call it \(\mathcal{C}_f\)
Proof(1)
Take the same objects: \(Ob(\mathcal{C}_f):=Ob(\mathcal{C})\)
\(\mathcal{C}_f(a,b) := f(\mathcal{C}(a,b))\)
Check this obeys the definition of an enriched category:
Condition on the monoidal unit:
\(I_W \leq f(I_V)\) — from the first condition of a monoidal monotone map.
\(\forall c \in Ob(\mathcal{C}): I_V \leq \mathcal{C}(c,c)\) — first condition of an enriched category, which \(\mathcal{C}\) is
\(\forall c \in Ob(\mathcal{C}):f(I_V) \leq f(\mathcal{C}(c,c))\) — monotone map property
\(\forall c \in Ob(\mathcal{C}):f(I_V) \leq \mathcal{C}_f(c,c)\) — definition of \(\mathcal{C}_f\)
\(\forall c \in Ob(C_f): I_W \leq C_f(c,c)\) — transitivity, using 1 and 4, noting \(Ob(\mathcal{C})=Ob(\mathcal{C}_f)\)
Condition on monoidal product:
\(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) = f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e))\) — definition of \(\mathcal{C}_f\)
\(f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e)) \leq f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e))\) — second condition of a monoidal monotone map
\(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e) \leq \mathcal{C}(c,e)\) — Second condition of an enriched category
\(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq f(\mathcal{C}(c,e)\) — monotone map property
\(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq \mathcal{C}_f(c,e)\) — definition of \(\mathcal{C}_f\)
\(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) \leq \mathcal{C}_f(c,e)\) — transitivity, 1,2 and 5
Linked by
Metric space to preorder(1)
Consider the function \([0,\infty] \xrightarrow{f} \mathbb{B}\) which maps 0 to true and otherwise to false.
Can check that f is monotonic and preserves the monoidal product+unit, so it is a monoidal monotone. (this was shown in Exercise 2.44)
Thus we have a tool to convert metric spaces into preorders.
Linked by
Exercise 2-67(2)
Recall the “regions of the world” Hausdorff metric space We learned that a metric space can be converted into a preorder by a particular monoidal monotone map. How would you interpret the resulting preorder?
Exercise 2-68(2)
Find a different monoidal monotone map \(\mathbf{Cost}\xrightarrow{g}\mathbf{Bool}\) from the one in Example 2.65. Using the construction from Proposition 2.64, convert a Lawvere metric space into two different preorders. Find a metric space for which this happens.NOCARD
Solution(1)
Take the two monoidal monotone maps from Exercise 2.44
f yields a discrete preorder whereas g does not.
Enriched functors(5)
V-functor(1)
A \(\mathcal{V}\) functor \(\mathcal{X}\xrightarrow{F}\mathcal{Y}\) between two \(\mathcal{V}\) categories
A function \(Ob(\mathcal{X})\xrightarrow{F}Ob(\mathcal{Y})\) subject to the constraint:
\(\forall x_1,x_2 \in Ob(\mathcal{X}): \mathcal{X}(x_1,x_2) \leq \mathcal{Y}(F(x_1),F(x_2))\)
Linked by
- Bool-functors: referenced
- Bool-functors: referenced
- Cost-functors: referenced
- Natural isomorphism of Bool-categories and preorders: referenced
- Feasibility relationships as Bool-profunctors: referenced
- V-profunctors: referenced
- V-profunctor: referenced
- Solution: referenced
- Companion and conjoint: referenced
- V-adjunction: referenced
- Exercise 4-41: referenced
Bool-functors(1)
Monotone maps, considering the source and target preorders as Bool-categories, are in fact Bool-functors.
The monotone map constraint, that \(x_1\ \leq_X\ x_2 \implies F(x_1)\leq_Y F(x_2)\), translates to the enriched category functor constraint, that \(\mathcal{X}(x_1,x_2) \leq \mathcal{Y}(F(x_1),F(x_2))\).
Cost-functors(1)
A Cost-functor is also known as a Lipschitz function.
Therefore a Lipschitz function is one under which the distance between any pair of points does not increase.
Exercise 2-73(2)
The concepts of opposite/dagger/skeleton extend from preorders to \(\mathcal{V}\) categories.
Recall an extended metric space \((X,d)\) is a Lawvere metric space with two extra properties.
Show that a skeletal dagger Cost-category is an extended metric space
Solution(1)
The skeletal dagger cost category has a set of objects, \(Ob(\mathcal{X})\) which we can call points.
For any pair of points, we assign a hom-object in \([0,\infty]\) (we can call this a distance function).
Skeletal property enforces the constraint \(d(x,y)=0 \iff x=y\).
The second enriched category property enforces the triangle inequality.
Because we have a dagger category, our distance function is forced to be symmetric.
Just like the information of a preorder is discarded (to yield a set) when we only consider skeletal dagger preorders, information must be discarded from Cost-categories to yield a Lawvere metric space.
Linked by
Product V-categories(6)
V-category product(1)
The \(\mathcal{V}\) product of two \(\mathcal{V}\) categories, \(\mathcal{X} \times \mathcal{Y}\)
This is also a \(\mathcal{V}\) category with:
\(Ob(\mathcal{X}\times\mathcal{Y}) := Ob(\mathcal{X})\times Ob(\mathcal{Y})\)
\((\mathcal{X} \times \mathcal{Y})((x,y),(x',y')) := \mathcal{X}(x,x') \otimes \mathcal{Y}(y,y')\)
Linked by
Cost-category product(1)
Let \(\mathcal{X}\) and \(\mathcal{Y}\) be the Lawvere metric spaces (i.e. Costcategories) defined by the following weighted graphs.
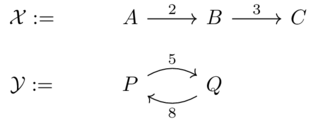
The product can be represented by the following graph:
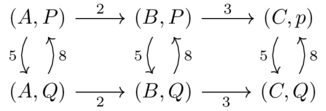
The distance between any two points \((x,y),(x',y')\) is given by the sum \(d_X(x,x)+d_Y(y,y)\).
We can also consider the Cost-categories as matrices
\(\mathcal{X}\) A B C A 0 2 5 B \(\infty\) 0 3 C \(\infty\) \(\infty\) 0 \(\mathcal{Y}\) P Q P 0 5 Q 8 0 \(\mathcal{X}\times\mathcal{Y}\) (A,P) (B,P) (C,P) (A,Q) (B,Q) (C,Q) (A,P) 0 2 5 5 7 10 (B,P) \(\infty\) 0 3 \(\infty\) 5 8 (C,P) \(\infty\) \(\infty\) 0 \(\infty\) \(\infty\) 5 (A,Q) 8 10 13 0 2 5 (B,Q) \(\infty\) 8 11 \(\infty\) 0 3 (C,Q) \(\infty\) \(\infty\) 8 \(\infty\) \(\infty\) 0 Can view this as a 2x2 grid of 3x3 blocks: each is a \(\mathcal{X}\) matrix shifted by \(\mathcal{Y}\).
Exercise 2-75(2)
Let \(\mathcal{X} \times \mathcal{Y}\) be the \(\mathcal{V}\)-product of two \(\mathcal{V}\) categories.
Check that for every object we have \(I \leq (\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)
Check that for every three objects we have:
\((\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_2,y_2)) \otimes (\mathcal{X} \times \mathcal{Y})((x_2,y_2),(x_3,y_3)) \leq (\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_3,y_3))\)
Solution(1)
By axioms of \(\mathcal{V}\) categories: \(I \leq \mathcal{X}(x,x')=xx\) and \(I \leq \mathcal{Y}(y,y')=yy\)
By monotonicity: \(I \leq xx \land I \leq yy\) implies \(I = I \otimes I \leq xx \otimes yy\).
By the definition of a product category this last term can be written as \((\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)
By axioms of \(\mathcal{V}\) categories: \(\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3) \leq \mathcal{X}(x_1,x_3)\) and \(\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3) \leq \mathcal{Y}(y_1,y_3)\)
Therefore, by monotonicity, we have \((\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3)) \otimes (\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3)) \leq \mathcal{X}(x_1,x_3) \otimes \mathcal{Y}(y_1,y_3)\)
Desugaring the definiton of the hom-object in \(\mathcal{X}\times\mathcal{Y}\), the property we need to show is that \((\mathcal{X}(x_1,x_2) \otimes\mathcal{Y}(y_1,y_2)) \otimes (\mathcal{X}(x_2,x_3) \otimes\mathcal{Y}(y_2,y_3)) \leq (\mathcal{X}(x_1,x_3) \otimes\mathcal{Y}(y_1,y_3))\)
Given the associativity and commutitivity of the \(\otimes\) operator, we can rearange the order and ignore parentheses for the four terms on the LHS. Do this to yield the desired expression.
Exercise 2-78(2)
Consider \(\mathbb{R}\) as a Lawvere metric space, i.e. as a Cost-category.
Form the Cost-product \(\mathbb{R}\times\mathbb{R}\).
What is the distance from \((5,6)\) to \((-1,4)\)?
Solution(1)
The distance is the Manhattan/\(L_1\) distance: \(|5-(-1)| + |6-4| = 8\)
Computing presented V-categories with matrix mult(33)
Monoidal closed preorders(11)
The term closed in the context of symmetric monoidal closed preorders refers to the fact that a hom-element can be constructed from any two elements (the preorder is closed under the operation of "taking homs").
Consider the hom-element \(v \multimap w\) as a kind of "single use v to w converter"
a and v are enough to get to w iff a is enough to get to a single-use v-to-w converter.
One may read
Closed SMP(1)
A symmetric monoidal preorder \(\mathcal{V}:=(V,\leq,I,\otimes)\) is symmetric monoidal closed (or just closed)
For every \(v,w \in V\), there is an element \(v \multimap w \in V\) called the hom-element with the property:
\(\forall a,v,w \in V: (a \otimes v) \leq w\) iff \(a \leq (v \multimap w)\)
Linked by
- Cost is closed: referenced
- Chemistry closed resource theory: referenced
- Chemistry closed resource theory: referenced
- SMP currying: referenced
- Proof: referenced
- Proof: referenced
- Proof: referenced
- Exercise 2-82: referenced
- Exercise 2-82: referenced
- Exercise 2-82: referenced
- Solution: referenced
- Solution: referenced
- Exercise 2-85: referenced
- Quantale: referenced
- Cost quantale: referenced
- Quantale is SMP with all joins: referenced
- Proof: referenced
- Proof: referenced
Self-enriched category(1)
A category \(\mathcal{V}\) that is enriched in itself.
For every \(v,w \in Ob(\mathcal{V})\) we can define \(\mathcal{V}(v,w)\) as \((v \multimap w) \in \mathcal{V}\)
For this to be an enrichment, we need to check the two conditions.
The first condition \(I \leq \mathcal{X}(x,x) = x \multimap x\) is satsified because \(I \otimes x \leq x\)
The second condition is satisfied by P2.87e
Linked by
Cost is closed(1)
The symmetric monoidal preorder \(\mathbf{Cost}:=([0,\infty],\geq,0,+)\) is monoidal closed.
For any \(x,y \in [0,\infty]\), define \(x \multimap y := max(0,y-x)\)
Then, for any \(a,x,y\), we have \(a+x\geq y\) iff \(a \geq y-x\) iff \(max(0,a)\geq max(0,y-x)\) iff \(a \geq (x \multimap y)\)
We can use this to define a notion of subtraction in Cost.
Linked by
Chemistry closed resource theory(1)
What would a monoidal closed structure mean for the resource theory of chemistry?
For any two material collections, one can form a material collection \(c \multimap d\) with the property that, for any a one has \(a + c \rightarrow d\) iff \(a \rightarrow (c \multimap d)\)
Concretely, say we have \(2 H_2O + 2 Na \rightarrow 2 NaOH + H_2\), we must also have \(2H_2O \rightarrow (2Na \multimap (2NaOH+H_2))\)
From two molecules of water, you can form a certain substance. This doesn’t make sense, so maybe this symmetric monoidal preorder is not closed.
Alternatively, think of the substance \(2Na \multimap (2NaOH+H_2)\) as a potential reaction, that of converting sodium to sodium-hyroxide+hydrogen. Two molecules of water unlock that potential. NOCARD
SMP currying(2)
Proof(1)
The meaning of \((- \otimes v) \dashv (v \multimap -)\) is exactly the condition of \(\multimap\) in a closed symmetric monoidal preorder.
This follows from (1), using the fact that left adjoints preserve joins.
This follows from (1) using the alternative characterization of Galois connections.
Alternatively, start from definition of closed symmetric monoidal preorder and substitute \(v \multimap w\) for \(a\), and note by reflexivity that \((v \multimap w) \leq (v \multimap w)\)
Then we obtain \((v \multimap w) \otimes v \leq w\) (by symmetry of \(\otimes\) we are done)
Since \(v \otimes I = v \leq v\), then the closed condition means that \(v \leq I \multimap v\)
For the other direction, we have \(I \multimap v = I \otimes (I \multimap v) \leq v\) by (3)
We need \(u \otimes (u \multimap v) \otimes (v \multimap w) \leq w\)
This follows from two applications of the third part of this proposition.
Suppose \(\mathcal{V}:=(V,\leq,I,\otimes,\multimap)\) is a closed symmetric monoidal preorder.
For every \(v \in V\) the monotone map \((V, \leq) \xrightarrow{-\otimes v}(V,\leq)\) is left adjoint to \((V, \leq)\ \xrightarrow{v \multimap -} (V,\leq)\)
For any element \(v \in V\) and a subset of elements \(A \subseteq V\), if the join \(\bigvee A\) exists, then so does \(\bigvee_{a \in A} v \otimes a\) and we have \((v \otimes \bigvee A)\cong \bigvee_{a \in A} v \otimes a\)
\(\forall v,w \in V: v \otimes (v \multimap w) \leq w\)
\(\forall v \in V: v \cong (I \multimap v)\)
\(\forall u,v,w \in V: (u \multimap v) \otimes (v \multimap w) \leq (u \multimap w)\)
Linked by
Exercise 2-82(2)
Prove that a symmetric monoidal preorder is closed iff, given any \(v \in V\), the map \(V \xrightarrow{(-\otimes v)}V\) given by multiply with v has a right adjoint. We write this adjoint \(V \xrightarrow{(v \multimap -)}V\):
Show that \(V \xrightarrow{(-\otimes v)}V\) is monotone.
Supposing that \(\mathcal{V}\) is closed, show that \(\forall v,w \in V: ((v \multimap w)\otimes v) \leq w\)
Show that \((v \multimap -)\) is monotone.
Conclude that a symmetric monoidal preorder is closed iff the monotone map \((- \otimes v)\) has a right adjoint.
Solution(1)
Given the monotonicity constraint of \(\otimes\)
And reflexivity: \(v \leq v\), we have:
\(x_1 \leq y_1\) implies that \((x_1 \otimes v) \leq (y_1 \otimes v)\)
Substitute \(v \multimap w\) for \(a\) into the closed property equation, to get \(((v \multimap w)\otimes v) \leq w \iff v \multimap w \leq v \multimap w\) (the RHS is true by reflexivity, so the LHS must be true).
Need to show: if we assume \(x \leq y\) then we can conclude \((v \multimap x) \leq (v \multimap y)\)
From the previous part, we have \((v \multimap x) \otimes v \leq x\) and \((v \multimap y) \otimes v \leq y\)
Assuming the antecedant \(x \leq y\), and given transitivity, we have \((v \multimap x) \otimes v \leq (v \multimap y) \otimes v\)
Because the \(\otimes\) operation must be monotonic, the consequent follows.
A Galois connection requires that both maps be monotone and that they satisfy \(f(p)\leq q\) iff \(p \leq g(q)\). This is the relation captured by the closed property equation, and both maps were shown to be monotone.
Exercise 2-85(2)
Show that \(\mathbf{Bool}=(\mathbb{B},\leq, true, \land)\) is monoidal closed.
Solution(1)
Our translation is: \(\otimes \mapsto \land,\ \leq \mapsto \implies\)
Condition for being closed is then:
\(\forall a,v,w:\) \((a \land v) \implies w\) iff \(a \implies (v \multimap w)\)
On the LHS, we have the truth table:
a v w \((a \land v) \implies w\) F F F T F F T T F T F T F T T T T F F T T F T T T T F F T T T T In order to define \(v \multimap w\) in a way consistent with this, we need it to only be false when \(v=true, w=false\), which is the truth condition for \(v \implies w\).
This is consistent with a ‘single use v-to-w converter’ analogy.
Linked by
Quantales(13)
Think of a unital, commutative, quantale as a kind of navigator.
A navigator understands ’getting from one place to another’
Different navigators understand different aspects (whether one can get from A to B, how much time it will take, ...)
What they share in common is that, given routes A to B and B to C, they understand how to get a route A to C.
Because of Proposition 2.96, a quantale has all meets and joins (even though we define it simply as having all joins).
Quantale(1)
A unital commutative quantale (or just quantale, in this book)
A symmetric monoidal closed preorder \(\mathcal{V}=(V,\leq,I,\otimes,\multimap)\) that has all joins.
\(\bigvee A\) exists for all \(A \subseteq V\)
Denote the empty join as \(0 := \bigvee \varnothing\)
Linked by
- Quantales: referenced
- Cost quantale: referenced
- Cost quantale: referenced
- Quantale is SMP with all joins: referenced
- Exercise 2-93: referenced
- Exercise 2-94: referenced
- Solution: referenced
- Quantale matrix: referenced
- Feasibility relationships as Bool-profunctors: referenced
- V-profunctor: referenced
- V-profunctor category: referenced
- Exercise 4-41: referenced
Cost quantale(1)
We saw that Cost is monoidal closed in Example 2.83
To check if Cost is a quantale, we take an arbitrary set of elements and ask if it has a join.
Because \(\geq\) is a total order, we can take the infimum or greatest lower bound, as the join.
\(\bigvee\{2.5,2.05,2.005,...\} = 2\).
We need a \(0\), which is something which is related to everything (the first join condition is vacuous). Because the preorder relation is \(\geq\) in Cost we need something greater than everything, so \(0 = \infty\).
Thus Cost is a quantale.
All joins implies all meets(2)
Let \((P,\leq)\) be a preorder. It has all joins iff it has all meets.
Proof(1)
Meets and joins are dual, so it suffices to prove one of the directions (the opposite category shows that having all meets having all joins, if we are able to prove that having all joins means having all meets in the original preorder).
Suppose there are all joins and \(A \subseteq P\) is a subset for which we want the meet.
Consider the set \(M_A := \{p \in P\ |\ \forall a \in A: p \leq a \}\) (everything below all of \(A\) - these are candidates for the meet of \(A\))
The first condition for the meet is satisfied by all. We get the actual meet by taking \(\bigvee M_A\) which is guaranteed to exist. Because this element is greater than or equal to all elements that are \(\leq A\), it satisfies the second condition for the meet.
Linked by
Quantale is SMP with all joins(2)
Suppose \(\mathcal{V}=(V,\leq,I,\otimes)\) is a symmetric monoidal preorder that has all joins.
Then \(\mathcal{V}\) is closed, i.e. has a \(\multimap\) operation and hence is a quantale, iff \(\otimes\) distributes over joins
i.e. if Eq (2) from P2.87 holds: \((v \otimes \bigvee A)\cong \bigvee_{a \in A} v \otimes a\).
Proof(1)
We proved one direction in P2.87
We need to show that \((v \otimes \bigvee A)\cong \bigvee_{a \in A} v \otimes a\) (and all joins existing) implies that there exists a \(\multimap\) operation that satisfies the closed property: \(\forall a,v,w \in V: (a \otimes v) \leq w\) iff \(a \leq (v \multimap w)\).
The adjoint functor theorem for preorders states that monotone maps preserve joins iff they’re left adjoint, so \(V \xrightarrow{-\otimes v} V\) must have a right adjoint g, which, being a Galois connection, will satisfy the property \((a \otimes v) \leq w \iff a \leq g(w)\) (this is the monoidal closed property).
Let’s rename \(g \equiv v \multimap -\). The adjoint functor theorem even gives us a construction for the right adjoint, namely: \(v \multimap w:=\bigvee\{a \in V\ |\ a \otimes v \leq w\}\).
Linked by
Exercise 2-92(2)
What is \(\bigvee \varnothing\), called \(0\), in the case of:
\(\mathcal{V}=\mathbf{Bool}=\{\mathbb{B},\leq, true,\land\}\)
\(\mathcal{V}=\mathbf{Cost}=([0,\infty],\geq,0,+)\)
What is the join \(x \vee y\) for Bool and Cost?
Solution(1)
\(False\) and \(\infty\) respectively
Logical or and \(min\) respectively
Exercise 2-94(2)
Recall the power set symmetric monoidal preorder \((P(S),\subseteq, S, \cap)\) Is this a quantale?
Solution(1)
Yes, \(0=\varnothing\) (it is related to everything) and the join of any pair of subsets is well-defined as their union. By Proposition 2.98, this means it is a quantale.
Matrix multiplication in a quantale(9)
The identity \(\mathcal{V}\) matrix, \(X \times X \xrightarrow{I_X} \mathcal{V}\) has \(I\) on the diagonal entries and \(0\) on the off-diagonal entries.
Quantale matrix(1)
A matrix with entries in \(\mathcal{V}\), where \(\mathcal{V}=(V, \leq, \otimes, I)\) is a quantale. (A \(\mathcal{V}\) matrix). Matrix multiplication between \(\mathcal{V}\) matrices
Need two sets, and function \(X \times Y \xrightarrow{M} V\). Call \(M(x,y)\) the (x,y)th entry.
We can multiply \(X \times Y \xrightarrow{M} V\) and \(Y \times Z \xrightarrow{N} V\) to get a new \(\mathcal{V}\) matrix \(X \times Z \xrightarrow{M*N} V\).
\((M*N)(x,z)(x,z)\) defined as \(\bigvee_y\ M(x,y)\otimes N(y,z)\)
Note that this is similar to the standard matrix multiplication, with \(\bigvee \mapsto \Sigma, \otimes \mapsto *\)*
Linked by
Abstract matrix multiplication(1)
Let \(\mathcal{V}=\mathbf{Bool}\). Here is matrix multiplication \(M*N\) with \(X=\bar{3}, Y=\bar{2},Z=\bar{3},M=X\times Y\rightarrow Z, N=Y\times Z\rightarrow B\).
\(X\)
| F | F |
|---|---|
| F | T |
| T | T |
\(Y\)
| T | T | F |
|---|---|---|
| T | F | T |
\(X*Y\)
| F | F | F |
|---|---|---|
| T | F | T |
| T | T | T |
Exercise 2-103(2)
Write the 2x2 identity matrices for each of the quantales:
\((\mathbb{N},\leq,1,*)\)
\(\mathbf{Bool}:=(\mathbb{B},\leq,true,\land)\)
\(\mathbf{Cost}:=([0,\infty],\leq,0,+)\)
Solution(1)
1 0 0 1 T F F T 0 \(\infty\) \(\infty\) 0
Exercise 2-104(2)
Let \(\mathcal{V}=(V,\leq,I,\otimes,\multimap)\) be a quantale. Prove:
The identity law
For all \(\mathcal{V}\) matrices \(X\times Y\xrightarrow{M}V\), one has \(I_X * M = M\)
The associative law
For any matrices \(W \times X \xrightarrow{M} V, X \times Y \xrightarrow{N} V, Y \times Z \xrightarrow{P} V\), one has \((M*N)*P=M*(N*P)\)
Solution(1)
\(\forall v \in \mathcal{V}\), we have \(0 \otimes v \cong 0\).
\(0 \otimes v\)
\(\cong v \otimes 0\) – symmetry
\(= v \otimes \bigvee_{a \in \varnothing} a\) – definition of \(0\)
\(\cong \bigvee_{a \in \varnothing} v \otimes a\) – \(-\otimes x\) preserves joins b/c it is left adjoint
\(= 0\) – definition of 0
Plug this into definition of matrix multiplication
\(I_X * M(x,y)\)
\(= \bigvee_{x'}I_x(x,x')\otimes M(x',y)\) – definition of matrix multiplication in a quantale
\(=(I_x(x,x)\otimes M(x,y))\vee(\bigvee_{x'\ne x}I_x(x,x')\otimes M(x',y))\) – split join into two cases
\(=(I\otimes M(x,y))\vee(\bigvee_{x'\ne x}0\otimes M(x',y))\) – Definition of identity matrix
\(=M(x,y)\vee 0\) – join of a singleton set
\(=M(x,y)\) – Zero is the least element in \(\mathcal{V}\)
Need to show \(\underset{y \in Y}\bigvee (\underset{x\in X}\bigvee M(w,x)\otimes N(x,y))\otimes P(y,z)\) is the same as \(\underset{x \in X}\bigvee M(w,x)\otimes(\underset{y \in Y}\bigvee N(x,y) \otimes P(y,z))\) for all \(w \in W,z \in Z\)
The associativity of \(\otimes\) and the fact it preserves joins b/c it is left adjoint lets us shift the symbols around appropriately.
Linked by
Exercise 2-105(2)
Consider the distance matrix represented by this graph from Exercise 2.60:

| \(\rightarrow\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 6 | 3 | 11 |
| B | 2 | 0 | 5 | 5 |
| C | 5 | 3 | 0 | 8 |
| D | 11 | 9 | 6 | 0 |
Compute the distance matrix by power iteration of the matrix of the presentation.
Solution(1)
| \(M\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | \(\infty\) | \(\infty\) | 3 |
| B | 2 | 0 | 5 | \(\infty\) |
| C | \(\infty\) | \(\infty\) | 0 | 6 |
| D | \(\infty\) | 3 | \(\infty\) | 0 |
| \(M^2\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 6 | \(\infty\) | 3 |
| B | 2 | 0 | 5 | 11 |
| C | \(\infty\) | 9 | 0 | 6 |
| D | 5 | 3 | 8 | 0 |
After this, \(M^n\) is the \(\rightarrow\) matrix
Chapter 3: Databases(120)
What is a database(3)
A database is a system of interlocking tables.
Some columns are internal references (i.e. foreign keys), others are external references (string, int, etc.).
Changing the internal reference value doesn’t mean anything (if we do it consistently), but not for the external references.
Category theory provides a mathmetical approach for translating between two different database representations of a common domain.
Exercise 3-3(2)
Count the number of non-ID columns in the following database and compare to the number of foreign keys in the database schema.
| Employee | FName | WorksIn | Mngr |
|---|---|---|---|
| 1 | Alan | 101 | 2 |
| 2 | Ruth | 101 | 2 |
| 3 | Kris | 102 | 3 |
| Dept | DName | Secr |
|---|---|---|
| 101 | Sales | 1 |
| 102 | IT | 3 |
Solution(1)
They are the same: 5
Categories(30)
Free Categories(7)
Category(1)
A category, \(\mathcal{C}\)
Need to specify a collection of objects, \(Ob(\mathcal{C})\)
For every two objects c and d, one specifies a set \(\mathcal{C}(c,d)\) called morphisms from c to d
This set is called the hom-set and morphism is a shorthand for homomorphism
For every object c one specifies a morphism \(id_c \in \mathcal{C}(c,c)\) called the identity morphism
For every pair of morphisms \(c \xrightarrow{f} d\) and \(d \xrightarrow{g} e\), one specifies a morphism \(c \xrightarrow{f;g}e\) called the composite of f and g
Furthermore, these must satisfy two conditions:
unitality: composing with identities does not change anything
associativity: \((f;g);h = f;(g;h)\)
Linked by
- Free category on a graph: referenced
- Naturals as category: referenced
- Exercise 3-19: referenced
- Functor: referenced
- Exercise 3-43: referenced
- Diagram: referenced
- Diagram: referenced
- Exercise 3-55: referenced
- Exercise 3-58: referenced
- Terminal object: referenced
- Cone: referenced
- Limit: referenced
- Finite limits in Set: referenced
- Limit formula: referenced
- Cocone: referenced
- Solution: referenced
- V-profunctor category: referenced
- Monoidal categories: referenced
- SMC: referenced
- Exercise 4-52: referenced
Free category on a graph(1)
Naturals as category(1)
The natural numbers as a free category: \(\boxed{\overset{\bullet}{z}\circlearrowleft s}\)
There are infinitely many paths, in bijection with the natural numbers.
This is a category with one object, also called a monoid.
The composition operation corresponds to the addition operation.
Unitality and associativity give us the usual constraints on a monoid.
Linked by
Exercise 3-10(2)
The free category \(3 := \mathbf{Free}(\boxed{\overset{v_1}\bullet \xrightarrow{f_1}\overset{v_2}{\bullet}\xrightarrow{f_2}\overset{v_3}{\bullet}})\) has three objects and six morphisms. Give the morphisms names and write out the composition operation in a 6x6 matrix. Which are the identities?
Solution(1)
Identities are 1,2,3
| \(\circ\) | 1 | 2 | 3 | f1 | f2 | f12 |
|---|---|---|---|---|---|---|
| 1 | 1 | f1 | f12 | |||
| 2 | 2 | f2 | ||||
| 3 | 3 | |||||
| f1 | f1 | f12 | ||||
| f2 | f2 | |||||
| f12 | f12 |
Categories via path equations(5)
We can add constraints to a free category which states that two paths are equal
Exercise 3-17(2)
Write down all the morphisms in the free category presented by the following diagram:
Solution(1)
A,B,C,D,f,h,g,i,j
Preorders and free categories - two ends of a spectrum(5)
Takeaway: A preorder is a category where every two parallel arrows are the same.
Any preorder can be considered a category, and any category can be crushed down into a preorder (called preorder reflection).
The objects are the elements of the set, and there is a single morphism between a and b iff \(a \leq b\)
Considering a preorder as a category is right adjoint to turning a category into a preorder by preorder reflection.
Every category presentation lies somewhere between the free category and the preorder reflection.
Exercise 3-21(2)
What equations are needed to add to the following graphs in order to present the associated preorders?
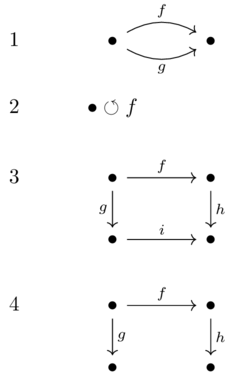
Solution(1)
f=g
f;f=f
f;h=g;i
none are needed
Exercise 3-22(2)
What is the preorder reflection of the category \(\mathbb{N}\) from Example 3.13
Solution(1)
The trivial preorder of one object.
Important categories in mathematics(3)
What are commonly called categories are actually Set-categories, in the terminology of \(\mathcal{V}\) categories.
There are many important categories:
Top - topological spaces (neighborhood)
Grph - graphs (connection)
Meas - measure spaces (amount)
Mon - monoids (action)
Grp - groups (reversible action, symmetry)
Cat - categories (action in context, structure)
The category Set(1)
The category of sets, denoted Set
Objects are the collection of all sets.
Morphisms are set-functions
Composition is function composition (satsifies associativity), identities are the identity functions (satisfies identity constraints).
Closely related is the subcategory FinSet of finite sets with morphisms being set-functions.
Opposite category(1)
Any category \(\mathcal{C}\) induces another category, \(\mathcal{C}^{op}\) defined as the same objects but all arrows reversed.
Isomorphisms in a category(10)
Isomorphisms formalize the notion of ‘interchangibility’, e.g. in a preorder the fact that \(a \cong b\) tells us that it doesn’t matter whether someone tells us \(c \leq a\) versus \(c \leq b\).
Isomorphism(1)
An isomorphism in a category
A morphism \(A \xrightarrow{f}B\) such that there exists a morphism \(B \xrightarrow{g}A\) satisfying \(f;g=id_A\) and \(g;f=id_B\)
We call f and g inverses and can write \(g=f^{-1}\)
We say A,B are isomorphic objects in this case.
Linked by
Set isomorphism(1)
The set \(\{a,b,c\}\) and \(\bar{3}\) are isomorphic (we have \(3!\) bijections to choose from). The isomorphisms in Set are the bijections.
Retraction(1)
It is possible for \(f;g=id\) but \(g;f \ne id\)
This is called a retraction rather than an isomorphism.
Exercise 3-31(2)
Show that the identity arrow on any given object is an isomorphism.
Solution(1)
The inverse to \(id_c\) exists; it is itself: \(id_c ; id_c = id_c\) (from the identity property)
Exercise 3-32(2)
A monoid in which every morphism is an isomorphism is known as a group
Is the natural numbers monoid a group?
Is the monoid with the added constraint \(s;s=z\) a group?
Solution(1)
No, \(s\) has no inverse (no natural number can be added to 1 to get 0)
Yes, this is the cyclic group with two elements.
Exercise 3-33(2)
Someone says that the only isomorphisms in \(\mathbf{Free}(G)\) for some graph \(G\) are the identity morphisms. Are they correct?
Solution(1)
They are correct. If we could compose \(f;g\) to get a morphisms from c to c, a free category would pick a new morphism rather than re-use the identity (which could be forced with a constraint).
Functors, natural transformations, and databases(33)
Sets and functions as databases(1)
We can think of sets as 1-table databases and functions as 2-table databases.
Any database takes a presentation of category, turns each vertex into a set and each arrow into a function.
Functors(11)
Functor(1)
A functor \(\mathcal{C}\xrightarrow{F}\mathcal{D}\) between two categories.
For each object in \(\mathcal{C}\) one specifies \(F(c) \in Ob(\mathcal{D})\)
For each morphism \(c_1\xrightarrow{f}c_2\) in \(\mathcal{C}\), one specifies \(F(c_1)\xrightarrow{F(f)}F(c_2)\) in \(\mathcal{D}\)
Furthermore, two properties must be satisfied:
Identity morphisms are mapped to identity morphisms
Composition is preserved: \(F(f;g)=F(f);F(g)\)
Linked by
- Exercise 3-40: referenced
- Solution: referenced
- Solution: referenced
- Exercise 3-43: referenced
- Exercise 3-43: referenced
- Exercise 3-43: referenced
- Exercise 3-43: referenced
- Solution: referenced
- Solution: referenced
- Database instance: referenced
- Database instance example: referenced
- Exercise 3-45: referenced
- Exercise 3-45: referenced
- Solution: referenced
- Natural transformation: referenced
- Diagram: referenced
- Functor category: referenced
- Natural transformation to unit: referenced
- Natural transformations between sequences: referenced
- Natural transformations between sequences: referenced
- Natural isomorphism of Bool-categories and preorders: referenced
- Exercise 3-55: referenced
- Exercise 3-58: referenced
- Instance homomorphism: referenced
- Grph as functor category: referenced
- Functor pullback: referenced
- Functor pullback: referenced
- DDS pullback: referenced
- DDS pullback: referenced
- DDS pullback: referenced
- DDS pullback: referenced
- Limit formula: referenced
Example between small categories(1)
Between the free square category and the commutative square category, there is no functor from the commutative square category to the free square category which keeps the corners in the same place.
If we did this, we’d have \(F(f;h)=F(g;i)\) (since these are the same morphism).
The functor rules would allow us to break this up into \(F(f);F(h)=F(g);F(i)\) and we don’t have a choice for those mappings other than \(f;h=g;i\), something that is not true in the free square category.
Functor between preorders(1)
Functors between preorders are monotone maps. Morphisms in the source must map to sources in the target, so if \(a \leq_P b\), then we require \(F(a) \leq_Q F(b)\), which is tantamount to the monotone map constraint.
Exercise 3-37(2)
How many functors are there from 2 to 3?
Solution(1)
We are only concerned about where the objects go, since the target category is a thin category (there is no choice about which morphism is mapped to). Thus the functors are: 11, 22, 33, 12, 23, 13
Exercise 3-39(2)
Say where each of the 10 morphisms in the free square category are mapped to by a functor to the commutative square category (where \(Ob(F)\) maps each corner to the same corner).
Solution(1)
The four identity morphisms and four length-1 paths are trivially mapped to the the corresponding morphisms. Both length-2 paths in the free category are mapped to the same morphism, \(f;h\).
Exercise 3-40(2)
Consider \(\mathcal{C}=\boxed{\bullet \rightarrow \bullet}\) and \(\mathcal{D}=\boxed{\bullet \rightrightarrows \bullet}\). Give two functors that act the same on objects but differently on morphisms.
Exercise 3-43(2)
Given a category \(\mathcal{C}\), show that there exists a functor \(id_\mathcal{C}\) known as the identity functor on \(\mathcal{C}\)
Show that given \(\mathcal{C}\xrightarrow{F}\mathcal{D}\) and \(\mathcal{D}\xrightarrow{G}\mathcal{E}\) we can define a new functor \(\mathcal{C}\xrightarrow{F;G}\mathcal{E}\) just by composing functions.
Show that there is a category, let’s call it Cat where the objects are categories, morphisms are functors, and identities/composition are given as above.
Solution(1)
Mapping objects and morphisms to themselves satsifies the functor constraints of preserving identities and composition.
If \(F,G\) both independently preserve identity arrows, then composition of these will also preserve this. Also \(G(F(f;g))=G(F(f);F(g))=G(F(f));G(F(g))\) using the independent facts that \(F,G\) each preserve composition.
Composition of identity functions do not change anything, so the identity functor (defined by identity function) will obey unitality. Because function composition is associative and functor composition is defined by this, we also satisfy that constraint.
Database instances as Set-valued functors(5)
Just like all sets are instances on the schema 1, all functions are instances on the schema 2.
Database instance(1)
A \(\mathcal{C}\) instance, where \(\mathcal{C}\) is a schema, i.e. a finitely-presented category.
A functor \(\mathcal{C} \xrightarrow{I} \mathbf{Set}\)
Linked by
Database instance example(1)
Consider the following category: \(\boxed{\overset{\bullet}{z}\circlearrowleft s\ \ \boxed{s;s = s}}\)
A functor from this category to Set is a set \(Z\) and a involution function \(Z \rightarrow Z\).
\(Z =\) natural numbers and a function sending everything to zero (zero is sent to zero)
\(Z =\) set of well-formed arithmetic expressions (e.g. \(12+(2*4)\)) and a function which evaluates to an integer (which itself is a well-formed expression). Evaluation on integers does nothing.
A function which sends numbers greater than 2 to their smallest prime factor (this is a no-op on the prime factors themselves).
Exercise 3-45(2)
Natural transformations(11)
Natural transformation(1)
A natural transformation \(F \overset{a}\Rightarrow G\) between two functors (going from \(\mathcal{C}\) to \(\mathcal{D}\)).
For each object \(c \in \mathcal{C}\), one specifies a morphism \(F(c)\xrightarrow{\alpha_c}G(c)\) in \(\mathcal{D}\) called the c-component of \(\alpha\)
These components must satisfy the naturality condition: for each morphism \(c \xrightarrow{f} d\) in \(\mathcal{C}\) we need \(F(f);\alpha_d=\alpha_c;G(f)\)
AKA this diagram should commute:
Linked by
- Functor category: referenced
- Small natural transformation example: referenced
- Natural transformation to unit: referenced
- Natural transformations between sequences: referenced
- Natural isomorphism of Bool-categories and preorders: referenced
- Exercise 3-55: referenced
- Exercise 3-55: referenced
- Solution: referenced
- Exercise 3-58: referenced
- Exercise 3-58: referenced
- Solution: referenced
- Instance homomorphism: referenced
- Grph as functor category: referenced
Diagram(1)
Functor category(1)
The functor category from categories \(\mathcal{C}\) to \(\mathcal{D}\)
\(\mathcal{D}^\mathcal{C}\) has all functors \(\mathcal{C} \rightarrow \mathcal{D}\) as objects and natural transformations as morphisms.
Linked by
Small natural transformation example(1)
The natural transformation requires us to choose morphisms in the righthand category for each object in the lefthand category
The only choices to satisfy the naturality condition are \(c\) and \(g\).
Natural transformation to unit(1)
Just like sets are in bijection with functors \(\mathbf{1}\rightarrow\mathbf{Set}\), we can also associate natural transformations
with functions.
In the language of functor categories, this claim is to say \(\mathbf{Set}^1\) is equivalent to \(Set\).
Linked by
Natural transformations between sequences(1)
Any non-decreasing sequence of naturals can be identified with a functor \(\mathbb{N}\rightarrow \mathbb{N}\), considering the preorder of naturals as a category.
A natural transformation between two of these functors would require a component \(\alpha_n\) for each natural, which means a morphism from \(F_n \rightarrow G_n\). This exists iff \(F(n)\leq G(n)\).
Thus we can put a preorder structure over the monotone map of \(\mathbb{N} \rightarrow \mathbb{N}\) (this is a thin functor category \(\mathbb{N}^\mathbb{N}\)).
Natural isomorphism of Bool-categories and preorders(1)
There exists a category PrO which has preorders as objects and monotone maps as morphisms.
There exists a category *Bool-Cat* in which the objects are Bool-categories and morphisms are Bool-functors.
We call these categories equivalent because there exist functors \(\mathbf{PrO}\overset{F}{\underset{G}{\rightleftarrows}}\mathbf{BoolCat}\) such that there exist natural isomorphisms \(F;G \cong id_\mathbf{PrO}\) and \(G;F \cong id_\mathbf{Bool-Cat}\)
Exercise 3-55(2)
Let’s investigate why the functor category is actually a category.
Figure out how to compose natural transformations \(F \xrightarrow{\alpha} G \xrightarrow{\beta}H\).
Propose an identity natural transformation on any functor and check that it is unital.
Solution(1)
The individual natural transformations satsifying the naturality condition makes the left and right squares commute, meaning the whole diagram commutes:
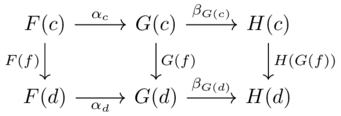
Thus the mapping from objects in \(F\)’s domain to morphisms in \(H\)’s codomain is given by \(G;\beta\).
Mapping each object to its own identity morphism will satisfy the naturality condition (all four edges of the square become identity functions). This will enforce unitality.
Exercise 3-58(2)
Let \(\mathcal{C}\) be an arbitrary category and \(\mathcal{P}\) be a preorder thought of as a category. Are the following true?
For any two functors \(\mathcal{C}\xrightarrow{F,G}\mathcal{P}\), there is at most one natural transformation \(F \rightarrow G\)
For any two functors \(\mathcal{P}\xrightarrow{F,G}\mathcal{C}\), there is at most one natural transformation \(F \rightarrow G\)
Solution(1)
This is true: there are no choices to be made for a natural transformation, given that for each morphism \(c\rightarrow d\) in \(\mathcal{C}\) we have to pick \(\alpha_c\) to be the morphism \(F(c)\rightarrow G(c)\) and \(\alpha_{d}\) to be the morphism \(F(d)\rightarrow G(d)\).
Counterexample:
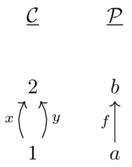
let \(F\) send \(f\mapsto x,a\mapsto1,b\mapsto 2\) and \(G\) maps everything to \(2\)
The naturality condition for f leaves us with two choices for \(\alpha_a\)
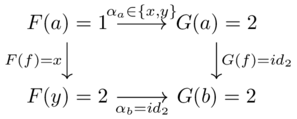
The category of instances on a schema(5)
Instance homomorphism(1)
An instance homomorphism between two database instances, \(\mathcal{C}\xrightarrow{I,J}\mathbf{Set}\)
A natural transformation between the two functors representing the instances.
\(\mathcal{C}\mathbf{Inst}:=\mathbf{Set}^\mathcal{C}\) denotes the functor category where these instance homomorphisms are the morphisms.
Grph as functor category(1)
The category of graphs as a functor category
Schema for graphs: \(\mathbf{Gr}:=\boxed{\overset{Arr}\bullet \overset{src}{\underset{tar}{\rightrightarrows}}\overset{Vert}\bullet}\)
A graph instance has a set of points and a set of arrows, each of which has a source and target.
There is a bijection between graphs and Gr instances
The objects of GrInst are graphs, the morphisms are graph homomorphisms (natural transformations between two Gr to Set functors)
Each graph homomorphism contains two components, which are morphisms in Set:
\(G(Vert) \xrightarrow{\alpha_{vert}} H(vert)\)
\(G(Arr) \xrightarrow{\alpha_{arr}} H(Arr)\)
Naturality conditions
Arrow table(1)
Consider the graphs \(G:=\boxed{\overset{1}\bullet \xrightarrow{a} \overset{2}\bullet \xrightarrow{b}\overset{3}\bullet}\) and \(H:=\boxed{\overset{4}\bullet \overset{d}{\underset{c}{\rightrightarrows}}\overset{5}\bullet\circlearrowleft e}\)
The arrow table of their database instances are below:
G src tar a 1 2 b 2 3 H src tar c 4 5 d 4 5 e 5 5
Linked by
Exercise 3-64(2)
Consider the graphs \(G,H\) from Example 3.63. We claim there is exactly one graph homomorphism such that \(\alpha_{Arr}(a)=d\). What is the other value of \(\alpha_{Arr}\), and what are the three values of \(\alpha_{Vert}\)?
Solution(1)
We need \(2 \mapsto 5\), so the source of \(\alpha_{Arr}(b)\) must be \(5\) (there is only one arrow to pick, \(e\)).
\(1 \mapsto 4,\ 2\mapsto 5,\ 3 \mapsto 5\)
Adjunctions and data migration(17)
Pulling back data along a functor(4)
Functor pullback(1)
The pullback of functor \(\mathcal{D}\xrightarrow{I}\mathbf{Set}\) along functor \(\mathcal{C}\xrightarrow{F}\mathcal{D}\)
The composite functor \(\mathcal{C}\xrightarrow{F;I}\mathbf{Set}\)
Given a natural transformation \(I \overset{\alpha}\Rightarrow J\), there is a natural transformation \(\alpha_F\) whose components (morphisms in Set from \((F;I)(c)\) to \((F;J)(c)\), for any \(c \in \mathcal{C}\) are given by: \((\alpha_F)_c := \alpha_{F(c)}\)
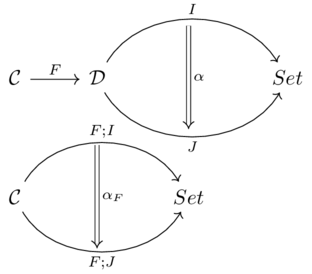
DDS pullback(1)
Pulling back data along a functor
We’ll migrate data between the graph-indexing schema Gr and the loop schema, called DDS (for discrete-dynamical system).
We’ll write down an example instance \(\mathbf{DDS}\xrightarrow{I}\mathbf{Set}\)
| State | Next |
|---|---|
| 1 | 4 |
| 2 | 4 |
| 3 | 5 |
| 4 | 5 |
| 5 | 5 |
| 6 | 7 |
| 7 | 6 |
We want to convert this state information into a graph that will let us visualize our machine.
Use the following functor \(F\):
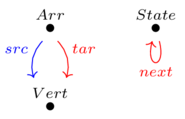
src is sent to identity
Can now generate a graph using the composite functor \(\mathbf{Gr}\xrightarrow{F}\mathbf{DDS}\xrightarrow{I}\mathbf{Set}\)
| Arr | src | tar |
|---|---|---|
| 1 | 1 | 4 |
| 2 | 2 | 4 |
| 3 | 3 | 5 |
| 4 | 4 | 5 |
| 5 | 5 | 5 |
| 6 | 6 | 7 |
| 7 | 7 | 6 |
\(Vert = \bar{7}\)
We can now draw the graph:
This procecure can be called “pulling back data along a functor". We pulled back data \(I\) along functor \(F\) (via functor composition).
Linked by
Exercise 3-67(2)
Consider the functor \(\mathbf{Gr}\xrightarrow{G}\mathbf{DDS}\) given by sending src to next and tar to id on State. Migrate the same data as in Example 3.65 and draw the corresponding graph.NOCARD
Solution(1)
| Arr | src | tar |
|---|---|---|
| 1 | 4 | 1 |
| 2 | 4 | 2 |
| 3 | 5 | 3 |
| 4 | 5 | 4 |
| 5 | 5 | 5 |
| 6 | 7 | 6 |
| 7 | 6 | 7 |
Adjunctions(6)
Adjoint functor(1)
A functor \(\mathcal{C}\xrightarrow{L}\mathcal{D}\) is left adjoint to a functor \(\mathcal{D}\xrightarrow{R}\mathcal{C}\)
For any \(c \in C\) and \(d \in D\), there is an isomorphism of hom-sets: \(\alpha_{c,d}: \mathcal{C}(c,R(d)) \xrightarrow{\cong} \mathcal{D}(L(c),d)\) that is natural in c and d.
Given a morphism \(c \rightarrow{f} R(d)\) in \(\mathcal{C}\), its image \(g:=\alpha_{c,d}(f)\) is called its mate (and vice-versa)
To denote the adjunction we write \(L \dashv R\) or
Linked by
Galois connections are adjoint(1)
Galois connections between preorders are the same as adjunctions between the corresponding categories.
Currying(1)
The adjunction called currying says \(\mathbf{Set}(A \times B,C)\cong \mathbf{Set}(A,C^B)\)
Linked by
Adjoint examples(1)
Examples of adjunctions
Free constructions: given a set you get a free groupmonoidring/vector space/etc. - each of these is a left adjoint. The corresponding right adjoint throws away the algebraic structure.
Given a graph you get a free preorder or a free category, the corresponding right adjoint is the underlying graph of a preorder/category.
Discrete things: given any set you get a discrete preordergraphmetric spacecategorytopological space/etc.; each of these is a left adjoint and the corresponding right adjoint again recovers the set.
Codiscrete things: given any set you get a codiscrete preorder, complete graph, codiscrete category, category, etc.; each of these is a right adjoint and the left adjoint gives the underlying set.
Given a group, you can quotient by its commutator subgroup to get an abelian group; this is a left adjoint. The right adjoint is the inclusion of abelian groups into Grp
Exercise 3-73(2)
Currying was an adjunction between functors in Set, but the example only discussed what the functors did to objects.
Given a morphism \(X \xrightarrow{f}Y\), what morphism should \(X \times B \xrightarrow{-\times B}Y\times B\) return?
Given a morphism \(X \xrightarrow{f}Y\), what morphism should \(X^ B \xrightarrow{(-)^B}Y^B\) return?
Consider \(\mathbb{N}\times \mathbb{N}\xrightarrow{+}\mathbb{N}\). Currying \(+\), we get a certain function \(\mathbb{N}\xrightarrow{p}\mathbb{N}^\mathbb{N}\). What is \(p(3)\)?
Solution(1)
This morphism maps \((x,b)\mapsto (f(x),b)\)
This morphism takes in a function \(B \xrightarrow{bx} X\) and composes with f to give \(B \xrightarrow{bx;f} Y\)
It takes a number and returns a function which adds three to that number.
Left and right pushforward functors(2)
Given \(\mathcal{C}\xrightarrow{F}\mathcal{D}\), the data migration functor \(\Delta_F\) turns \(\mathcal{D}\) instances to \(\mathcal{C}\) instances. This functor has both a left and right adjoint:

| Migration Functor | Pronounced | Reminiscent of | Database idea |
|---|---|---|---|
| \(\Delta\) | Delta | Duplicate or destroy | Duplicate or destroy tables or columns |
| \(\Sigma\) | Sigma | Sum | Union (sum up) data |
| \(\Pi\) | Pi | Product | Pair and query data |
Plane tickets(1)
Consider a functor which discards the distinction between Economy and First Class seats in an airplane.
The \(\Delta\) functor is uninteresting - it will copy the rows for Seat into both Economy and First class.
The functor \(\Pi\) puts into each airline seat only seats which are in both the Economy and First Class tables with the same price and position.
The functor \(\Sigma\) puts all Economy and First Class seats into the Seat table and discards the information of from which table they came from.
Single set summaries of databases(5)
Emails(1)
Consider the schema \(\mathfrak{g} := \boxed{\overset{Email}\bullet \overset{sentBy}{\underset{receivedBy}{\rightrightarrows}} \overset{Address}\bullet}\)
And an example instance: \(\mathfrak{g}\xrightarrow{I}\mathbf{Set}\)
| SentBy | ReceivedBy | |
|---|---|---|
| 1 | Bob | Grace |
| 2 | Grace | Pat |
| 3 | Bob | Emmy |
| 4 | Sue | Doug |
| 5 | Doug | Sue |
| 6 | Bob | Bob |
Data migration functors \(\Sigma_!,\Pi_!\) go from \(\mathcal{C}\) Inst to 1-Inst, but we showed that 1-Inst is equivalent to Set in Example 3.53.
\(\Sigma_!\) tells us the mailing groups, the "connected components" in \(I\):
| 1 |
|---|
| Bob-Grace-Pat-Emmy |
| Sue-Doug |
\(\Pi_!\) tells us the emails that were sent from a person to themselves
1 \(Em_6\) (Bob)
Linked by
Exercise 3-76(2)
For any category \(\mathcal{C}\) there is exactly one functor to the category 1, let’s call it \(!\) Where does it send each object and each morphism?
Solution(1)
There is only one object to send each object to and only one morphism to send each morphism to. Because everything in the target is equal to everything else, all functor constraints are trivially satisfied.
Exercise 3-78(2)
Draw the instance \(I\) in Example 3.77 as a graph.NOCARD
Solution(1)
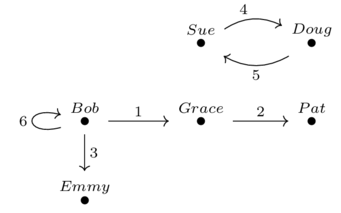
Introduction to limits and colimits(37)
Terminal objects and products(17)
Terminal object(1)
terminal object in a category \(\mathcal{C}\)
An object z is terminal if, for each object c there exists a unique morphism \(c \xrightarrow{!} z\)
We say terminal objects have a universal property
Linked by
Product(1)
Given two objects \(X,Y \in \mathcal{C}\), the product \(X \times Y\)
This is another object in \(\mathcal{C}\) with morphisms \(X \xleftarrow{p_x}X\times Y\xrightarrow{p_y}Y\)
This should satisfy the property that there exists a unique morphism making the following diagram commute for any other object C and morphisms \(X \xleftarrow{f}C\xrightarrow{g}Y\)
Linked by
Terminal in Set(1)
In Set, any set with exactly one element is a terminal object. For an arbitrary other set, we have no choice but to send everything to that one object when specifying a function.
Product in Set(1)
In Set, the categorical product of two sets is our usual cartesian product.
The projections are \(x \xrightarrow{p_x}(x,y)\xrightarrow{p_y}y\)
The unique morphism from some \(X \xleftarrow{f} C \xrightarrow{g} Y\), the unique map \(C \xrightarrow{!}X \times Y\) is given by \((f\times g)(c):=(f(c),g(c))\).
Product in Cat(1)
The product of two categories \(\mathcal{C}\times \mathcal{D}\) may be given as follows:
\(Ob(C\times D)\) are the pairs \((c,d)\) where c is an object of \(\mathcal{C}\) and d is an object of \(\mathcal{D}\).
Morphisms are pairs \((c,d)\xrightarrow{(f,g)}(c',d')\) where \(c \xrightarrow{f}c'\) is a morphism in \(\mathcal{C}\) and \(d \xrightarrow{g}d'\) is a morphism in \(\mathcal{D}\).
Composition is given by composing each entry in the pair separately.
Linked by
Terminal objects are isomorphic(2)
Proof(1)
Suppose \(Z,Z'\) are both terminal objects. Therefore there exist unique maps \(Z \overset{a}{\underset{b}{\rightleftarrows}}Z'\)
Composing these we get \(Z \xrightarrow{a;b} Z\), but this is forced to be the identity map because there is only one morphism from \(Z\) to itself and we have to have an identity.
Therefore we can talk about ’the terminal object’ as if there were only one.
All terminal objects in a category \(\mathcal{C}\) are isomorphic
Exercise 3-81(2)
Let \(z \in P\) be an element of a preorder, and consider the corresponding category \(\mathcal{P}\). Show that z is a terminal object iff it is a top element in \(P\), i.e. \(\forall c \in P: c \leq z\)
Exercise 3-82(2)
Name a terminal object in the category Cat
Solution(1)
1 is terminal because a functor from any other category is forced to map all objects to 1 and all morphisms to its identity morphism.
Exercise 3-83(2)
Name a category which does not have a terminal object
Solution(1)
The category corresponding to the natural numbers has no terminal object (it would be an integer larger than all integers).
Exercise 3-88(2)
Let \(x,y \in P\) be elements of a preorder and \(\mathcal{P}\) be the corresponding category. Show that the product \(x \times y\) in \(\mathcal{P}\) agrees with their meet \(x \land y\) in \(P\).
Solution(1)
The uniqueness aspect of the product is not relevant since all morphisms are unique in a preorder category.
The product definition translates to an operation which takes a pair of objects in a preorder and gives us another object with the property that \(x \times y \leq x\) and \(x \times y \leq y\), and for any other b that also has this property we have \(b \leq x\times y\)
Considering the set \(A=\{x,y\}\), the conditions for \(x \times y\) matches the definition of \(\bigwedge A\) (grestest lower bound).
Exercise 3-90(2)
What are identity morphism in a product category \(\mathcal{C}\times \mathcal{D}\)?
Why is composition in a product category associative?
What is the product category \(1 \times 2\)?
What is the product category of two preorders?
Solution(1)
For object \((c,d)\), the identity morphism is \((id_c,id_d)\)
The operation was defined in terms of function composition which is associative.
It is isomorphic to just 2
The underlying set is the cartesian product, and \((a,b)\leq(a',b')\) iff \(a \leq a' \land b \leq b'\)
Limits(8)
How is the product (and its unique map) related to terminal objects?
Call \(\mathbf{Cone}(X,Y)\) the /category of cones over X and Y in/ \(\mathcal{C}\), given two objects in \(\mathcal{C}\).
An object is pair of maps \(X \xleftarrow{f}C\xrightarrow{g}Y\) for some \(c \in \mathcal{C}\)
A morphism a from \(X \xleftarrow{f}C\xrightarrow{g}Y\) to \(X \xleftarrow{f'}C\xrightarrow{g'}Y\) is a morphism \(C \rightarrow C'\) in \(\mathcal{C}\) such that the following diagram commutes:
Free diagram(1)
Suppose \(\mathcal{J}\) is the free category on the graph \(\boxed{1 \rightarrow 2 \leftarrow 3 \rightrightarrows 4 \rightarrow 5}\)
We may draw a diagram \(\mathcal{J}\xrightarrow{D}\mathcal{C}\) inside \(\mathcal{C}\) as below:
\(\boxed{D_1 \rightarrow D_2 \leftarrow D_3 \rightrightarrows D_4 \rightarrow D_5}\)
We can represent this diagram as a cone over the diagram by picking a \(C \in \mathcal{C}\) for which every pair of parallel paths that start from \(C\) are the same.
Terminal object as limit(1)
Terminal objects are imits where the indexing category is empty, \(\mathcal{J}=0\).
Product as limit(1)
Products are limits where the indexing category consists of two objects with no arrows, \(\mathcal{J}=\boxed{\overset{v}\bullet\ \overset{w}\bullet}\).
Linked by
Cone(1)
A cone \((C,c_*)\) over a diagram \(\mathcal{J}\xrightarrow{D}\mathcal{C}\) and the category \(\mathbf{Cone}(D)\)
We require:
An object \(C \in Ob(\mathcal{C})\)
For each object \(j \in \mathcal{J}\), a morphism \(C \xrightarrow{c_j}D(j)\).
The following property must be satisfied:
\(\forall f \in \mathcal{J}(j,k):\) \(c_k=c_j;D(f)\)
A morphism of cones is a morphism \(C \xrightarrow{a} C'\) in \(\mathcal{C}\) such that, for all \(j \in \mathcal{J}\), we have \(c_j=a;c'_j\).
Cones and their morphisms form a category.
Linked by
Limit(1)
The limit of a diagram \(D\), \(lim(D)\)
The limit of \(D\), denoted is the terminal object in the category \(\mathbf{Cone}(D)\)
If \(lim(D)=(C,c_*)\) we refer to \(C\) as the limit object and the map \(c_j\) as the jth projection map
Linked by
Exercise 3-91(2)
Check that the product \(X \xleftarrow{p_X} X \times Y \xrightarrow{p_Y} Y\) is terminal object in \(\mathbf{Cone}(X,Y)\)
Solution(1)
The existence and uniqueness of the morphism to the product object in the product definition are the conditions of being a terminal object in \(\mathbf{Cone}(X,Y)\). The maps of the terminal object to \(X\) and \(Y\) are the projection maps of the product.
Finite limits in Set(9)
This section shows that a database instance \(\mathcal{J}\xrightarrow{I}\mathbf{Set}\) is a diagram in Set. Also the functor \(\Pi_!\) takes the limit of this diagram.
Details not presented, but it suffices to work with just the finitely-presented graph of \(\mathcal{J}\) rather than the category itself (path equations not relevant for this).
Limit formula(2)
Let \(\mathcal{J}\) be a category presented by the finite graph \((\{v_1,...,v_n\},A,s,t)\) with some equations.
Let \(\mathcal{J}\xrightarrow{D}\mathbf{Set}\) be some set-valued functor.
The set \(\underset{\mathcal{J}}{lim}D := \{(d_1,...,d_n)\ |\ \forall i: d_i \in D(v_i)\ \text{and}\ \forall v_i\xrightarrow{a}v_j \in A: D(a)(d_i)=d_j\}\)
... together with projection maps \(lim_\mathcal{J}D \xrightarrow{p_i}D(v_i)\) given by \(p_i(d_1,...,d_n):=d_i\)
... is a limit of \(D\). NOCARD
Proof(1)
NOT PROVEN
Linked by
Terminal object in limit formula(1)
With respect to Proposition 3.95, if \(\mathcal{J}=0\), then \(n=0\); there are no vertices.
There is exactly one empty tuple which vacuously satisfies the properties, so we’ve constructed the limit as the singleton set \(\{()\}\) consisting of just the empty tuple.
Thus the limit of the empty diagram, i.e. the terminal object in Set, is the singleton set.
Pullback diagram(1)
If \(\mathcal{J}\) is presented by the cospan graph \(\boxed{\overset{x}\bullet \xrightarrow{f} \overset{a}\bullet \xleftarrow{g}\overset{y}\bullet}\) then its limit is known as a pullback.
Given the diagram \(X \xrightarrow{f}A\xleftarrow{g}Y\), the pullback is the cone shown below:
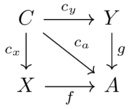
Because the diagram commutes, the diagonal arrow is superfluous. One can denote pullbacks instead like so:
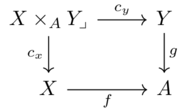
The pullback picks out the \((X,Y)\) pairs which map to the same output.
Exercise 3-97(2)
Show that the limit formula works for products in Set
The diagram, whose limit is a product, is \(\mathcal{J}=\boxed{\overset{v}\bullet\ \overset{w}\bullet}\) (see Exaample 3.94)
Solution(1)
\(V=\{v,w\}, A=\varnothing\)
The second condition of the set comprehension is vacuously satisfied because \(A = \varnothing\)
So all we have left is all pairs of tuples where the first element comes from \(D(v)\) and the second element comes from the set \(D(w)\).
This is the Cartesian product \(D(v) \times D(w)\)
Exercise 3-99(2)
If \(1 \xrightarrow{D}\mathbf{Set}\) is a functor, what is the limit of \(D\)? Compute using the limit formula and check answer against the limit definition.
A brief note on colimits(3)
Cocone(1)
A cocone in a category \(\mathcal{C}\)
A cone in \(\mathcal{C}^{op}\)
Given a diagram \(\mathcal{J}\xrightarrow{D}\mathcal{C}\), we may take the limit of the functor \(\mathcal{J}^{op}\xrightarrow{D^{op}}\mathcal{C}^{op}\) is a cocone in \(\mathcal{C}\) - the colimit of \(D\) is this cocone.
Exercise 3-101(2)
Let \(\mathcal{C}\xrightarrow{F}\mathcal{D}\) be a functor. How should we define its opposite: \(\mathcal{C}^{op}\xrightarrow{F^{op}}\mathcal{D}^{op}\)
Solution(1)
There is an isomorphism between a category and its opposite, meaning there are natural functors \(\overset{\cong}\rightarrow\) which alternate between them.
Define \(\mathcal{C}^{op}\xrightarrow{F^{op}}\mathcal{D}^{op}\) as \(F ; \overset{\cong}\rightarrow\). This is a valid functor as it is the composition of two functors.
Chapter 4: Co-design(77)
Can we build it(1)
A large project is broken down into subprojects, each of which can be broken down into further subprojects.
Each subproject provides resources (or ‘functionalities’) but also requires resources.
There are interdependencies; if subteam A needs more space in order to provide a resource for B, B may need to use less space, causing a ripple effect.
Codesign diagrams have wires which represent a preorder of resources.
Boxes correspond to feasibility relations which match resource production with requirements
For every pair (p,r), where \(P\) is the preorder of resources to be produced and \(R\) is the preorder of resources to be required, the box says true or false for that pair.
I.e. “yes I can provide p given r" or “No, I cannot provide p given r"
I.e. Feasibility relations define a function \(P \times R \xrightarrow{\Phi}\mathbb{B}\) subject to some conditions
A co-design problem, represented by a co-design diagram, asks us to find the composite of some feasibility relations.
Enriched profunctors(22)
Feasibility relationships as Bool-profunctors(6)
Whenever you have 10 W of power, you also have 5 W (\(5 W \leq 10 W\))
The requirement that the feasibility relation map is monotone says that if \(x' \leq_X x\) and \(y \leq_Y y'\), then \(\phi(x,y) \leq_{Bool} \phi(x',y')\)
If x can be obtained from y, something easier to obtain than x can also be obtained from y
If x can be obtained from y, then x can be obtained from something harder to obtain than y
This chapter should make the following table clear:
Bool- Bool- Bool- Bool is a quantale, meaning it has all joins and a closure operation, \(\mathbb{B}\times\mathbb{B}\xrightarrow{\Rightarrow}\mathbb{B}\). The closure operation must satisfy \(b \land c \leq d\) iff \(b \leq (c \Rightarrow d)\). It is the fact that Bool is a quantale that makes this chapter work; we could alternatively use Cost and obtain the cost of obtaining \(x\) from \(y\), not just whether or not it’s possible.
Feasilibiliy relation(1)
A feasibility relation for preorder \(X\) given preorder \(Y\)
A monotone map \(X^{op}\times Y \xrightarrow{\phi} \mathbf{Bool}\)
Also denoted \(X \overset{\phi}\nrightarrow Y\)
Given \(x \in X, y \in Y\), if \(\phi(x,y)=true\) then we say x can be obtained from y
Linked by
- Can we build it: referenced
- Feasibility relationships as Bool-profunctors: referenced
- Feasibility relationships as Bool-profunctors: referenced
- Exercise 4-10: referenced
- Back to co-design diagrams: referenced
- Movie constraints: referenced
- Movie constraints: referenced
- Composing Bool-profunctors: referenced
- The categories V-Prof and Feas: referenced
Exercise 4-4(2)
Suppose we have the preorders \(X:=\boxed{monoid\rightarrow category \leftarrow preorder}, Y:=\boxed{nothing \rightarrow thisBook}\)
Draw the Hasse diagram for the preorder \(X^{op} \times Y\)
Write a profunctor \(X \overset{\phi}\nrightarrow Y\)
True means “my aunt can explain an x given y"
Interpret the fact that the preimage of true is an upper set in \(X^{op}\times Y\)
Solution(1)
Let \(\phi((M,B))=\phi((P,B))=True\) else \(False\)
The preimage of true being an upper set is a consequence of monotone maps to Bool. The domain orders combinations by feasibility (\(x\leq y\) means x is easier than y), and the preimage being an upper set says that if my aunt can explain \(x\) given \(y\), then she can do something easier than \(x\) given \(y\) and can explain \(x\) with something with more explanatory power than \(y\).
Exercise 4-7(2)
Show that the Boolean \(\Rightarrow\) satsifies the requirements of a closure operator.
Solution(1)
This boils down to the tautology that \((a \land v) \implies w\) iff \(a \implies (v \implies w)\), where the last \(\implies\) comes from \(\multimap\) and the others come from \(\leq\).
V-profunctors(12)
A \(\mathcal{V}\) functor must have \(\mathcal{V}\) categories for domain and codomain, so the \(\mathcal{V}\) of a \(\mathcal{V}\) profunctor must be considered as enriched in itself.
Matrix algorithm for computing distance matrix of profunctor: \(d_X * M_\phi * d_Y\)
V-profunctor(1)
A \(\mathcal{V}\) profunctor, denoted \(\mathcal{X}\overset{\phi}{\nrightarrow} \mathcal{Y}\) - where \(\mathcal{V}=(V,\leq,I,\otimes)\) is a (unital commutative) quantale, and \(\mathcal{X},\mathcal{Y}\) are \(\mathcal{V}\) categories.
A \(\mathcal{V}\) functor \(\mathcal{X}^{op}\times Y \xrightarrow{\phi} \mathcal{V}\)
Linked by
- Feasibility relationships as Bool-profunctors: referenced
- V-profunctors: referenced
- Bool-profunctors: referenced
- Bool-profunctors: referenced
- Bool-profunctors: referenced
- Bool-profunctors: referenced
- Cost-profunctors: referenced
- Cost-profunctors: referenced
- Exercise 4-10: referenced
- Exercise 4-9: referenced
- V-profunctor composition: referenced
- Exercise 4-22: referenced
- V-profunctor category: referenced
- Unitality of unit profunctor: referenced
- V-profunctor collage: referenced
- Exercise 4-44: referenced
Bool-profunctors(1)
Bool-profunctors and their interpretation as bridges
Let’s consider Bool-profunctors. Recall a preorder (Bool-category) can be drawn as a Hasse diagram.
A Bool-profunctor \(X \overset{\phi}{\nrightarrow} Y\) can look like this:

With bridges coming from the profunctor, one can now use both paths to get from points in \(X\) to points in \(Y\).
There is a path from N to e, so \(\phi(N,e)=\)\(true\) but \(\phi(W,d)=\)\(false\).
We could put a box around both preorders and define a new preorder, called the collage.
Linked by
Cost-profunctors(1)
Cost profunctors and their interpretation as bridges.
Cost categories are Lawvere metric spaces and can be represented by weighted graphs
This is a depiction of a Cost-profunctor
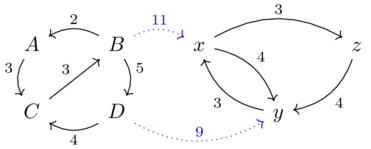
The distance from a point in the left to a point in the right will run through the left, across a bridge, then through through the right.
\(\phi(B,x)=\)\(11\),\(\phi(A,z)=\)\(20\),\(\phi(C,y)=\)\(17\)
Linked by
Exercise 4-10(2)
Is it true that a Bool-profunctor is exactly the same as a feasibility relation?
Solution(1)
Monotone maps are Bool-functors between Bool-categories, so the definitions line up
Exercise 4-12(2)
Exercise 4-15(2)
Fill out the Cost-matrix associated with Example 4.13 NOCARD
Solution(1)
| \(\phi\) | x | y | z |
|---|---|---|---|
| A | 17 | 21 | 20 |
| B | 11 | 15 | 14 |
| C | 14 | 18 | 17 |
| D | 12 | 9 | 15 |
Exercise 4-9(2)
Show that a \(\mathcal{V}\) profunctor is the same as a function \(Ob(\mathcal{X})\times Ob(\mathcal{Y}) \xrightarrow{\phi} V\) such that, \(\forall x,x' \in \mathcal{X}, y,y' \in \mathcal{Y}\), the following holds in \(\mathcal{V}\):
\(\mathcal{X}(x',x)\otimes \phi(x,y) \otimes \mathcal{Y}(y,y') \leq \phi(x',y')\)
Solution(1)
A \(\mathcal{V}\) profunctor must be a function satisfying the following constraint, according to the \(\mathcal{V}\) functor definition:
\(Z((x,y),(x',y')) \leq\) \(\mathcal{V}(\phi((x,y)),\phi((x',y')))\)
where \(Z = \mathcal{X}^{op}\times \mathcal{Y}\)
Unpacking the definition of a product \(\mathcal{V}\) category, we obtain
\(\mathcal{X}^{op}(x,x') \otimes \mathcal{Y}(y,y') \leq \mathcal{V}(\phi((x,y)),\phi((x',y')))\)
And applying opposite category definition: \(\mathcal{X}(x',x) \otimes \mathcal{Y}(y,y') \leq \mathcal{V}(\phi((x,y)),\phi((x',y')))\)
Noting the definition of \(\multimap\) for a \(\mathcal{V}\) category enriched in itself:
\(\mathcal{V}(v,w)=v\multimap w\), so now we have: \(\mathcal{X}(x',x) \otimes \mathcal{Y}(y,y') \leq \phi((x,y)) \multimap \phi((x',y'))\)
From the constraint of a hom-element of a symmetric monoidal preorder \(\mathcal{V}\), i.e. \(a \leq (v \multimap w)\) iff \((a \otimes v) \leq w\), we see that the first case pattern matches with:
\(a \mapsto\) \(\mathcal{X}(x',x) \otimes \mathcal{Y}(y,y')\)
\(v \mapsto\) \(\phi((x,y))\)
\(w \mapsto\) \(\phi((x',y'))\)
So using the iff we can rewrite as \((a \otimes v) \leq w\), and use the commutativity of \(\otimes\) to obtain the desired expression.
Linked by
Back to co-design diagrams(4)
Each box in a codesign problem has a list of preorders on the LHS and another list on the right.

The box represents a feasibility relation: \(Load \times Velocity \nrightarrow Torque \times Speed \times \$\)
Movie constraints(1)
Consider the feasibility relation
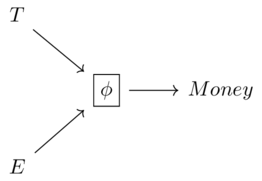
\(T:=\boxed{mean\rightarrow nice}\)
\(E:=\boxed{boring\rightarrow funny}\)
\(Money:=\boxed{100 K\rightarrow 500 K \rightarrow 1M}\)
A possible feasibility relation is here:
This says, e.g., a nice but boring movie costs $500,000 to produce.
We can infer that we can also make a mean/boring movie with what we can produce nice/boring movie.
Linked by
Exercise 4-18(2)
The node \((nice,funny)\) has no arrow from it in Example 4.18a. What does this mean?
Solution(1)
It is not feasible, for any amount of money listed, to produce a nice and funny movie.
Categories of profunctors(27)
Composing profunctors(4)
V-profunctor composition(1)
The composite \(\mathcal{X}\overset{\phi;\psi}\nrightarrow \mathcal{Z}\) of two \(\mathcal{V}\) profunctors, \(\mathcal{X}\overset{\phi}\nrightarrow\mathcal{Y}\) and \(\mathcal{Y}\overset{\psi}\nrightarrow\mathcal{Z}\)
\((\phi;\psi)(x,z) = \bigvee_Y(\phi(x,y)\otimes\psi(y,z))\)
Linked by
Composing Bool-profunctors(1)
Need a formula for composing two feasibility relations in series.
Suppose \(P,Q,R\) are cities (preorders) and there are bridges (hence, feasibility matrices).
The feasibility matrices are:
\(\textcolor{blue}{\phi}\) a b c d e N T F T F F E T F T F T W T T T T F S T T T T T \(\textcolor{red}{\psi}\) x y a F T b T T c F T d T T e F F Feasibility from \(P\) to \(R\) means there is a way-point in Q which is both reachable from \(p \in P\) and can reach \(r \in R\).
Composition is a union \((\phi;\psi)(p,r):= \bigvee_Q \phi(p,q)\land \psi(q,r)\).
But this is tantamount to matrix multiplication which gives us the result matrix:
\(\phi;\psi\) x y N F T E F T W T T S T T
Exercise 4-22(2)
Consider the following Cost profunctors \(\textcolor{blue}{\phi},\textcolor{red}{\psi}\) \[\begin{tikzcd}[ampersand replacement=\&] A \arrow[d, "3"', bend right] \& B \arrow[l, "2"', bend right] \arrow[d, "5", bend left] \arrow[r, "11", blue, dotted, bend left] \& x \arrow[rr, "3", bend left] \arrow[rd, "4", bend left] \& \& z \arrow[ld, "4", bend left] \arrow[r, "4", red,dotted, bend left] \arrow[rd, red, "4", dotted, bend right] \& p \arrow[r, "2", bend left] \& q \arrow[d, "2", bend left] \\ C \arrow[ru, "3"] \& D \arrow[l, "4", bend left] \arrow[rr, blue, "9", dotted, bend right] \& \& y \arrow[lu, "3", bend left] \arrow[rrr, red, "0", dotted, bend right=49] \& \& d \arrow[u, "1", bend left] \& r \arrow[l, "1", bend left] \end{tikzcd}\]
Fill in the matrix for the composite profunctor.
Solution(1)
| \(\phi;\psi\) | p | q | r | s |
|---|---|---|---|---|
| A | 23 | 25 | 21 | 22 |
| B | 17 | 19 | 15 | 16 |
| C | 20 | 22 | 18 | 19 |
| D | 11 | 13 | 9 | 10 |
The categories V-Prof and Feas(12)
Because Feas is a category, we can describe feasibility relation using one-dimensional wiring diagrams:
\(\xrightarrow{a}\boxed{f}\xrightarrow{b}\boxed{g}\xrightarrow{c}\boxed{h}\xrightarrow{d}\)
We need more structure to talk about multi-input/output case.
This chapter restricts discussion to skeletal quantales, but it is not hard to extend to non-skeltal ones. Two ways:
Let morphisms of \(\mathbf{Prof}_\mathcal{V}\) be isomorphism classes of \(\mathcal{V}\) profunctors. (analogous to trick used when defining Cospan category.)
We could relax what we mean by category (requiring composition to be unital/associative ‘up to isomorphism’ ... this is known as bicategory theory).
V-profunctor category(1)
The category \(\mathbf{Prof}_\mathcal{V}\), given a skeletal quantale \(\mathcal{V}\)
Objects: \(\mathcal{V}\) categories
Morphisms: \(\mathcal{V}\) profunctors, composed according to Definition 4.21
Identities are unit profunctors
Linked by
The category Feas(1)
The category Feas
Instantiate a \(\mathbf{Prof}_\mathcal{V}\) category with \(\mathcal{V}=\mathbf{Bool}\)
The unit profunctor(1)
Unitality of unit profunctor(2)
Proof(1)
Due to skeletality, we need to show for all inputs that \(\phi \leq U_P;\phi\) and \(U_P;\phi \leq \phi\) (the second equality to show is done similarly).
Forward direction
\(\phi(p,q) = I \otimes \phi(p,q)\)
due to unitality of \(I\) in a symmetric monoidal preorder.
\(\leq P(p,p) \otimes \phi(p,q)\)
This is because \(\forall p \in P:\) \(I \leq P(p,p)\) (a constraint of a \(\mathcal{V}\) category), the reflexivity of \(\leq\) for \(\phi(p,q)\), and the monotonicity of \(\otimes\).
\(\leq \underset{p' \in P}\bigvee(P(p,p') \otimes \phi(p',q))\)
The join is a least upper bound, and the LHS is an element of the set being joined over (the case where \(p=p'\)).
\(= (U_P;\phi)(p,q)\)
This is the profunctor composition formula, subtituting in the unit profunctor definition explicitly.
Reverse direction
Need to show \(\underset{p' \in P}\bigvee(P(p,p')\otimes \phi(p',q)) \leq \phi(p,q)\)
Show that this property holds for each \(p' \in P\) - given the join is a least upper bound, it will also be less than or equal to \(\phi(p,q)\)
\(P(p,p')\otimes\phi(p',q) = P(p,p')\otimes\phi(p',q)\otimes I\)
due to unitality of \(I\) in a symmetric monoidal preorder.
\(\leq P(p,p')\otimes \phi(p',q)\otimes Q(q,q)\)
\(\forall p:\) \(I \leq P(p,p)\) (a constraint of a \(\mathcal{V}\) category) and the monotonicity of \(\otimes\).
\(\leq\phi(p,q)\)
This was shown in Exercise 4.9
The unit profunctor is unital, i.e. for any profunctor \(P \overset{\phi}\nrightarrow Q\): \(U_P;\phi = \phi = \phi; U_Q\)
Linked by
Exercise 4-26(2)
Choose a nontrivial Cost-category \(\mathcal{X}\) and draw a bridge-style diagram of the unit profunctor \(\mathcal{X} \overset{U_\mathcal{X}}\nrightarrow \mathcal{X}\)
Solution(1)
becomes
Exercise 4-30(2)
Justify all steps the proof of the unitality of unit profunctors.
In the case of \(\mathcal{V}=\mathbf{Bool}\) show each step in the forward direction is actually an equality. NOCARD
Solution(1)
Done, see the proof
\(\forall p: P(p,p)=true\) for a Bool-enriched category, because that is the only option for \(I=true\leq P(p,p)\)
\(true \land x = x\)
If \(\phi(p,q)\):
then at least one element of the set being joined over is true (where \(p=p'\) such that \(P(p,p')\land \phi(p',q) = true\)), and the least upper bound of such a set is \(true\)
Else:
Then every element of that set is \(false\) such that the join is also \(false\).
If \(p\leq p'\), it fails because of the second conjunct (consider the constraint on profunctors: we are demanding equal or more resources than something we know fails)
If \(p \not \leq p'\), it fails because of the first conjunct. In a Bool-category \(P\), \(P(a,b)\) iff \(a \leq b\).
Exercise 4-31(2)
Prove that the serial composition of profunctors, \(\mathcal{X}\overset{\phi}\nrightarrow\mathcal{Y}\) and \(\mathcal{Y}\overset{\psi}\nrightarrow\mathcal{Z}\), is associative.
Solution(1)
This is tantamount to the quantale matrix multiplication being associative, which was shown in Exercise 2.104.
Fun profunctor facts - companions, conjoints, collages(11)
Companion and conjoint(1)
The companion and conjoint of a \(\mathcal{V}\) functor, \(\mathcal{P}\xrightarrow{F}\mathcal{Q}\)
Companion, denoted \(\mathcal{P}\overset{\hat F}\nrightarrow \mathcal{Q}\), is defined \(\hat{F}(p,q):=\mathcal{Q}(F(p),q)\)
Conjoint, denoted \(\mathcal{Q}\overset{\check{F}}\nrightarrow\mathcal{P}\)
Linked by
V-adjunction(1)
A \(\mathcal{V}\) adjunction.
A pair of \(\mathcal{V}\) functors, \(\mathcal{P}\overset{F}{\underset{G}\rightleftarrows} \mathcal{Q}\) such that: \(\forall p\in \mathcal{P}, q \in \mathcal{Q}: \mathcal{P}(p,G(q)) \cong \mathcal{Q}(F(p),q)\)
V-profunctor collage(1)
The collage of a \(\mathcal{V}\) profunctor, \(\mathcal{X}\overset{\phi}\nrightarrow \mathcal{Y}\)
A \(\mathcal{V}\) category, denoted \(\mathbf{Col}(\phi)\)
\(Ob(\mathbf{Col}(\phi)):=\)\(Ob(\mathcal{X})\sqcup Ob(\mathcal{Y})\)
\(\mathbf{Col}(\phi)(a,b) :=\) \(\begin{cases}\mathcal{X}(a,b) & a,b \in \mathcal{X} \\ \phi(a,b)& a \in \mathcal{X}, b \in \mathcal{Y} \\ \varnothing & a \in \mathcal{Y}, b \in \mathcal{X} \\ \mathcal{Y}(a,b) & a,b \in \mathcal{Y} \end{cases}\)
There are obvious functors \(\mathcal{X}\xrightarrow{i_\mathcal{X}}\mathbf{Col}(\phi)\) and \(\mathcal{Y}\xrightarrow{i_\mathcal{Y}}\mathbf{Col}(\phi)\) sending each object to “itself" called collage inclusions
Linked by
Companion and conjoint of identity(1)
For any preorder \(\mathcal{P}\), there is an identity functor \(\mathcal{P}\xrightarrow{id}\mathcal{P}\)
Its companion and conjoint agree: \(\hat{id}=\check{id}=\mathcal{P}\overset{U_\mathcal{P}}\nrightarrow \mathcal{P}\) equivalent to the unit profunctor.
Companion and conjoint of addition(1)
Consider the addition function on real numbers.
It is monotonic, since \((a,b,c)\leq(a',b',c')\) means \(a+b+c\leq a'+b'+c'\)
Therefore it has a companion and a conjoint
The companion \(\mathbb{R}\times\mathbb{R}\times\mathbb{R}\overset{\hat +}\nrightarrow \mathbb{R}\) sends (a,b,c,d) to true iff \(a+b+c\leq d\).
Linked by
Example 4-43 todo(1)
TODO
Exercise 4-36(2)
Check that the companion \(\hat{id}\) of the identity functor is actually the unit profunctor.
Solution(1)
TODO
Exercise 4-38(1)
Considering the addition example, what is the conjoint of this addition function?
Solution(0)
TODO
Exercise 4-44(1)
Draw a Hasse diagram for the collage of the profunctor:
Solution(0)
TODO
Categorification(15)
The basic idea(2)
General idea: take a thing we know and add structure to it such that things that were formerly properties become structures
Do in such a way as to be able to recover the thing we categorified by forgetting the new structure.
In categorified world, we have more structure available to talk about the relationships between objects.
An example is how we treated preorders as categories.
Ordinary categories are Set-categories
Categorification of arithmetic(1)
Categorification of arithmetic using the category FinSet
Replace natural numbers with arbtirary sets of that cardinality.
Replace \(+\) with coproduct.
This is good categorification because, with replacements, arithmatic truths are preserved: \(\bar{5}\sqcup \bar{3} \cong \bar{8}\)
A reflection on wiring diagrams(1)
To do...
Monoidal categories(6)
Just like preorders are special kinds of categories, symmetric monoidal preorders are special kinds of monoidal categories.
Just as we can consider \(\mathcal{V}\) categories for a symmetric monoidal preorder, we can consider \(\mathcal{V}\) categories when \(\mathcal{V}\) is a monoidal category.
One difference is that associativity is up to isomorphism: e.g. products in set \(S \times (T \times U)\) vs \((S \times T) \times U\)
When the isomorphisms of a symmetric monoidal category are replaced with equalities, we call it strict
Due to "Mac Lane’s coherence theorem" we can basically treat all as strict...something we implicitly do when writing wiring diagrams.
SMC(1)
A rough definition of a symmetric monoidal structure on a category \(\mathcal{C}\)
Two additional constituents
An object \(I \in Ob(\mathcal{C})\) called the monoidal unit
A functor \(\mathcal{C}\times \mathcal{C}\xrightarrow{\otimes}\mathcal{C}\) called the monoidal product
Subject to the well-behaved, natural isomorphisms
\(I \otimes c \overset{\lambda_c}\cong c\)
\(c \otimes I \overset{\rho_c}\cong c\)
\((c \otimes d)\otimes e \overset{\alpha_{c,d,e}}\cong c \otimes (d\otimes e)\)
\(c \otimes d \overset{\sigma_{c,d}}\cong d \otimes c\)
A category equipped with these is a symmetric monoidal category
Linked by
Set as SMC(1)
Monoidal structure on Set
Let \(I\) be any singleton, say \(\{1\}\) and the monoidal product is the cartesian product.
This means that \(\times\) is a functor:
For any pair of sets in \((S,T) \in Ob(\mathbf{Set}\times\mathbf{Set})\), one obtains a set \(S \times T \in Ob(\mathbf{Set})\).
For any pair of morphisms (functions) one obtains a function \((f\times g)\) which works pointwise: \((f\times g)(s,t):=(f(s),g(t))\) which preserves identities and composition.
The bookkeeping isomorphisms are obvious in Set
Linked by
Exercise 4-48(1)
Check that monoidal categories generalize monoidal preorders: a monoidal preorder is a monoidal category \((P,I,\otimes)\) where \(P(p,q)\) has at most one element.
Solution(0)
TODO
Exercise 4-50(2)
Consider the monoidal category \((\mathbf{Set},1,\times)\) together with the following diagram TODO - NEED TO COPY HERE
\(A=B=C=D=F=G=\mathbb{Z}\) and \(E=\mathbb{B}\)
\(f_C(a)=|a|\),
\(f_D(a)=a*5\),
\(g_E(d,b)=d\leq b\)
\(g_F(d,b)=d-b\)
\(h(c,e)=\text{if }e\text{ then }c\text{ else }1-c\)
Suppose the whole diagram defines a function \(A \times B \xrightarrow{q} G \times F\)
Answer:
What are \(g_E(5,3)\) and \(g_F(5,3)\)?
What are \(g_E(3,5)\) and \(g_F(3,5)\)?
What is \(h(5,true)\)?
What is \(h(-5,true)\)?
What is \(h(-5,false)\)?
What are \(q_G(-2,3)\) and \(q_F(-2,3)\)?
What are \(q_G(2,3)\) and \(q_F(2,3)\)?
Solution(1)
\(False,\ 2\)
\(True,\ -2\)
\(5\)
\(-5\)
\(6\)
\((2,-13)\) ... \(a\mapsto -2,\ b \mapsto 3,\ c\mapsto 2,\ d\mapsto -10,\ e\mapsto true,\ f\mapsto -13, g \mapsto 2\)
\((-1,7)\) ... \(a\mapsto 2,\ b \mapsto 3,\ c \mapsto 2,\ d\mapsto 10,\ e\mapsto false, f\mapsto 7, g\mapsto -1\)
Categories enriched in a symmetric monoidal category(6)
We said that ordinary categories were just Set-categories, but our definition of \(\mathcal{V}\) categories required the \(\mathcal{V}\) to be a preorder!
We have to generalize (categorify) \(\mathcal{V}\) categories.
Symmetric monoidal preorders can be considered as symmetric monoidal categories, despite not providing the data for identities and composition (these are not needed because there is no choice).
Example of property becoming structure: \(I \leq \mathcal{X}(x,x)\) is a property of \(\mathcal{V}\) categories as defined earlier but become part of the structure in the categorified version of the definition.
Enrichment in a SMC(1)
A \(\mathcal{V}\) category (a category enriched in \(\mathcal{V}\)) where \(\mathcal{V}\) is a symmetric monoidal category.
Call the category \(\mathcal{X}\). There are four constituents:
A collection of objects, \(Ob(\mathcal{X})\)
For every pair in \(Ob(\mathcal{X})\) one specifies the hom-object \(X(x,y) \in \mathcal{V}\).
For every object, specify a \(I \xrightarrow{id_x}X(x,x) \in \mathcal{V}\) called the identity element
For every pair of compatible morphisms, a \(\mathcal{X}(x,y)\otimes\mathcal{X}(y,z)\xrightarrow{;}\mathcal{X}(x,z)\) called the composition morphism.
These satisfy the usual associative and unital laws.
Linked by
Exercise 4-52(2)
Recall the example with Set as a symmetric moniodal category. Apply the definition of a \(\mathcal{V}\) category and see if this agrees with the definition of an ordinary category. Is there a subtle difference?
Solution(1)
We’ve replaced the identity morphisms with maps from the monoidal unit, but that is functionally equivalent to ‘just picking one’ given that the initial object is a singleton.
Exercise 4-54(2)
What are identity elements in Lawvere metric spaces (Cost-categories)? How do we interpret this in terms of distances?
Solution(1)
\(0\) was the monoidal unit - the distance from an object to itself.
Profunctors form a compact closed category(12)
Compact closed categories(7)
Dual object in a SMC(1)
The dual for an object \(c \in Ob(\mathcal{C})\), which is part of a symmetric monoidal category \((\mathcal{C},I,\otimes)\).
Three consituents:
An object \(c^* \in Ob(\mathcal{C})\) called the dual of c
A morphism \(I\xrightarrow{\eta_c}c^* \otimes c\) called the unit for c
A morphism \(c \otimes c^* \xrightarrow{\epsilon_c}I\) called the counit for c
These are required to satisfy two commutative diagram relations (snake equations)
and
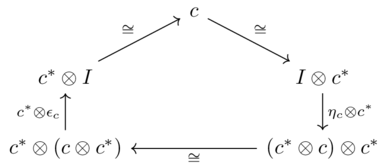
Linked by
Compact closed SMC(1)
A compact closed symmetric monoidal category
One for which every object there exists a dual. This allows us to use the following morphisms without reservation:
and
This also allows us to use the following snake equations in wiring diagrams without reservation:

and
Linked by
Compact closed properties(2)
If \(\mathcal{C}\) is a compact closed category, then:
\(\mathcal{C}\) is monoidal closed
the dual of c is unique up to isomorphism
\(c \cong (c^*)^*\)
Proof(1)
Not really proven, but: \(c \multimap d\) is given by \(c^* \otimes d\)
The natural isomorphism \(\mathcal{C}(b \otimes c, d)\cong \mathcal{C}(b,c \multimap d)\) is given by precomposing with \(id_b \otimes \eta_c\)
Correl as CCC(1)
The compact closed category: Corel
A correlation \(A \rightarrow B\) is an equivalence relation on \(A \sqcup B\)
Correlations are composed by the following rule: two elements are equivalent in the composite if we may travel from one to the other while staying within the component equivalence classes of either
There is a symmetric monoidal structure \((\varnothing, \sqcup)\). For any finite set A there is an equivalence relation on \(A \sqcup A\) that partitions elements in the first set from the second. The unit and counit are given by this partition:
\(\varnothing \xrightarrow{\eta_A} A \sqcup A\)
\(A \sqcup A \xrightarrow{\epsilon_A} \varnothing\)
Linked by
Exercise 4-62(2)
Draw a picture of the unit correlation \(\varnothing \xrightarrow{\eta_{\bar 3}} \bar 3 \sqcup \bar 3\)
Draw a picture of the counit correlation \(\bar 3 \sqcup \bar 3 \xrightarrow{\epsilon_{\bar 3}} \varnothing\)
Check that the snake equations hold. Since every object is its own dual, only one has to be checked.
Solution(1)
\(\boxed{\varnothing}\rightarrow \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\ \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\)
\(\boxed{\varnothing}\leftarrow \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\ \underset{\bar 3}{\boxed{\bullet\ \bullet\ \bullet}}\)
TODO
Feas as as compact closed category(5)
CCC from profunctor category(2)
Let \(\mathcal{V}\) be a skeltal quantale. The category \(\mathbf{Prof}_\mathcal{V}\) can be given the structure of a compact closed category, with the monoidal product given by the product of \(\mathcal{V}\) categories.
Proof(1)
Monoidal product acts on objects:
\(\mathcal{X} \times \mathcal{Y}((x,y),(x',y'))\) := \(\mathcal{X}(x,x') \otimes \mathcal{Y}(y,y')\)
Monoidal product acts on morphisms:
\(\phi \times \psi((x_1,y_1),(x_2,y_2))\) := \(\phi(x_1,x_2)\otimes\psi(y_1,y_2)\)
Monoidal unit is the \(\mathcal{V}\) category \(1\)
Duals in \(\mathbf{Prof}_\mathcal{V}\) are just opposite categories
For every \(\mathcal{V}\) category, \(\mathcal{X}\), its dual is \(\mathcal{X}^{op}\)
The unit and counit look like identities
The unit is a \(\mathcal{V}\) profunctor \(1 \overset{\eta_\mathcal{X}}\nrightarrow \mathcal{X}^{op} \times \mathcal{X}\)
Alternatively \(1 \times \mathcal{X}^{op} \times \mathcal{X}\xrightarrow{\eta_\mathcal{X}}\mathcal{V}\)
Defined by \(\eta_\mathcal{X}(1,x,x'):=\mathcal{X}(x,x')\)
Likewise for the co-unit: \(\epsilon_\mathcal{X}(x,x',1):=\mathcal{X}(x,x')\)
Exercise 4-64(1)
TODO
Solution(1)
TODO
Exercise 4-65(1)
TODO
Solution(0)
TODO
Exercise 4-66(1)
Check that the proposed unit and counits do obey the snake equations.
Solution(0)
TODO
Linked by
Chapter 5: Signal flow graphs(19)
Comparing systems as interacting signal processors(1)
Cyber-physical systems have tightly interacting physical and computational parts
Model system behavior as the passing around and processing of signals (e.g. real numbers).
Interaction can be thought of as variable sharing
Physical coupling between train cars forces their velocity to be the same
Categorical treatment of co-design problem allowed us to evaluate composite feasibility relation from a diagram of simpler feasibility relations.
Likewise we can evaluate whether two different signal flow graphs specify the same composite system
(perhaps to validate that a system meets a given specification)
Symmetric monoidal preorders were a special class of symmetric monoidal category where morphisms are constrained to be simple (at most one between any pair of objects).
Signal flow diagrams can be modeled by props, which is a special class of symmetricf monoidal category where objects are constrained to be simple (all are generaated by the monoidal product of a single object).
In the former we have to label wires but not boxes. Vice-versa for props.
Props and presentations(18)
Props - definition and first examples(13)
Each object is the n-fold monoidal product of the generating object \(1\).
To specify a prop \(P\) it is enough to specify 5 things (and check they satisfy the rules for symmetric monoidal categories):
A set \(\mathcal{C}(m,n))\) of morphisms \(m \rightarrow n\) for \(m,n \in \mathbb{N}\).
For all naturals, an identity map \(n \xrightarrow{id_n} n\)
For all \(m,n \in \mathbb{N}\), a symmetry map \(m+n \xrightarrow{\sigma_{m,n}} n+m\)
A composition rule: given \(m \xrightarrow f n\) and \(n \xrightarrow g p\), a map \(m \xrightarrow{f;g} p\)
A monoidal product on morphisms: given \(m \xrightarrow f m'\) and \(n \xrightarrow g n'\), a map \(m+n \xrightarrow{f+g} m' +n'\)
Prop(1)
A prop
A symmetric strict monoidal category \((\mathcal{C}, 0,+)\) for which \(Ob(\mathcal{C})=\mathbb{N}\) and the monoidal product on objects is given by addition.
Linked by
Prop functor(1)
A \(\ref{Prop|\emph{prop|referenced}}\) functor \(\mathcal{C} \xrightarrow F \mathcal{D}\) A functor for which
\(\forall n \in \mathbb{N}: F(n)=n\)
For all \(m_1 \xrightarrow f m_2\) and \(n_1 \xrightarrow g n_2 \in \mathcal{C}\): \(F(f))+F(g)=F(f+g) \in \mathcal{D}\)
Linked by
FinSet as prop(1)
The prop FinSet
Morphisms \(m \xrightarrow f n\) are functions from \(\bar m\) to \(\bar n\).
The identities, symmetries, and composition rule are obvious.
The monoidal product on functions is given by the disjoint union.
Linked by
Bij as prop(1)
Correl as prop(1)
The compact closed category \(\ref{Correl as CCC|\textbf{Corel|referenced}}\) is a prop.
Rel as prop(1)
There is a prop Rel
Morphisms are relations \(R \subseteq \bar m \times \bar n\)
Composition with \(S \subseteq \bar n \times \bar p\) is
\(\{(i, k)\ |\ \exists (i, j) \in R \land \exists (j,k) \in S\}\)
Monoidal product is given by the coproduct, which amounts to placing the two relations side-by-side.
Linked by
Bij FinSet prop functor(1)
The inclusion \(\mathbf{Bij} \overset{i}{\hookrightarrow} \mathbf{FinSet}\) is a prop functor.
There is a prop functor \(\mathbf{Bij} \xrightarrow F \mathbf{Rel_{Fin}}\) defined by \(F(\bar{m} \xrightarrow{f} \bar{n}):=\{(i,j)\ |\ f(i)=j\} \in \bar m \times \bar n\)
Exercise 5-5(1)
Draw a morphism \(3 \xrightarrow f 2\) and a morphism \(2 \xrightarrow g 4\) in \(\ref{FinSet as prop|\textbf{FinSet|referenced}}\)
Draw \(f+g\)
What is the natural composition rule for morphisms in \(\ref{FinSet as prop|\textbf{FinSet|referenced}}\)
What are the identities in \(\ref{FinSet as prop|\textbf{FinSet|referenced}}\)
Draw a symmetry map \(\sigma_{m,n}\) for some \(m,n\) in \(\ref{FinSet as prop|\textbf{FinSet|referenced}}\).
Solution(0)
TODO
Exercise 5-9(2)
A posetal prop is a prop that is also a poset.
In other words, a symmetric monoidal preorder \((\mathbb{N}, \leq)\) for some posetal relation \(\leq\), where the monoidal product is addition.
Give three examples of a posetal prop.
Solution(1)
The normal meaning of \(\leq\) as less than or equal to
The divisibility relation
The opposite of the first example (greater than or equal to).
Linked by
The prop of port graphs(5)
Port graph(1)
A port graph
A special type of prop where morphisms are open, directed, acyclic port graphs \((V, in, out, i)\)
\(V\) is a set of vertices
functions \(V \xrightarrow{in, out} \mathbb{N}\) give the in degree and out degree of each vertex
A bijection \(\bar m \sqcup O \xrightarrow{i} I \sqcup \bar n\), where \(I = \{(v,i)\ |\ v \in V, 1 \leq i \leq in(v)\}\) and \(O=\{(v,i)\ |\ v \in V, 1 \leq i \leq out(v))\}\) are the vertex inputs and vertex outputs, respectively.
Furthermore, an acyclicity condition:
Use the bijection \(i\) to construct the internal flow graph: a graph with an arrow \(u \xrightarrow{e^{u,i}_{v,j}} v\) for every \(i,j \in \mathbb{N}\) such that \(i(u,i)=(v,j)\)
This graph must be acyclic
Linked by
Port graph example(1)
A \((2,3)\) port-graph. [Draw this]
Since the overall type is \((2,3)\) we know we need a box with two overall inputs and three overall outputs.
There are three internal boxes, meaning the vertex set is \(\{a, b, c\}\).
\(in(a)=1\) and \(out(a)=3\) which tells us to draw one port on the LHS and three on the RHS.
The bijection \(i\) tells us how the ports are connected by wires.
The acyclic internal flow graph is shown below [TODO Draw this]
Linked by
Port graph category(1)
A category PG whose objects are natural numbers and morphisms are port graphs
We can compose a \((m,n)\) port graph with a \((n, p)\) port graph \((V \sqcup V',[in,in'],[out,out'], i'')\)
\(V \sqcup V' \xrightarrow{[in,in']} \mathbb{N}\) maps elements of \(V\) according to \(in\) and elements of \(V'\) according to \(in'\) (likewise for out).
The bijection \(\bar m \sqcup O \sqcup O' \xrightarrow{i''} I \sqcup I' \sqcup \bar p\) is defined as \(i''(x)=\begin{cases}i(x) & i(x) \in I \\ i'(i(x))& i(x) \in \bar n \\ i'(x) & x \in O' \end{cases}\)
The identity port graph on \(n\) is \((\varnothing, !, !, id_{\bar n})\) where \(\varnothing \xrightarrow{!} \mathbb{N}\) is a unique function.
This category is a prop.
The monoidal product of two portgraphs... TODO
Linked by
Exercise 5-16(2)
Describe how port graph composition looks, with respect to the visual representation of Example 5.14, and give a nontrivial example
Solution(1)
Todo